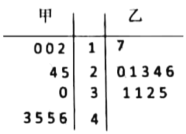
题目内容
【题目】已知正项数列
满足
，
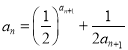则下列正确的是（ ）
A.当
时，
递增，
递增
B.当时，递增，递减
C.当
时，递增，递减
D.当时，递减，递减
【答案】B
【解析】
设
，画出函数的图像，利用数形结合的观点即可得到答案.
解：设，单调递减，画出图像如图所示：
由图像知
，所以对于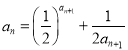
当
时，不妨确定
的位置，根据，把
标到图上，如图所示：
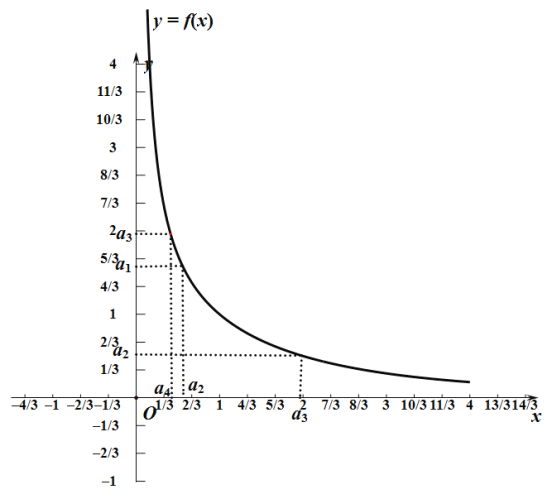
由
图像知，
，所以
，所以
，一直根据图像推下去可得：对于数列
，所以奇数项
，所有偶数项
.
从作图过程可以看出：
，
所以可得：数列
递增数列，
递减数列.
当
时，不妨确定的位置，根据，把标到图上，如图所示：
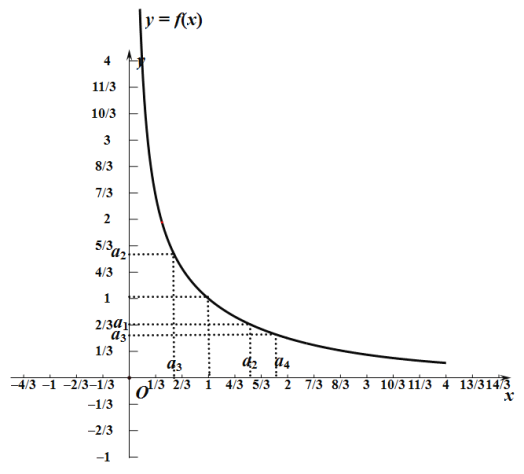
由图像知，
，所以
，一直根据图像推下去可得：对于数列，所以奇数项
，所有偶数项
.
从图像可以看出：
，
所以：数列递减数列，递增数列.
故选：B.
【题目】某学校为了调查学生数学素养的情况，从初中部、高中部各随机抽取100名学生进行测试.初中部的100名学生的成绩（单位：分）的频率分布直方图如图所示.
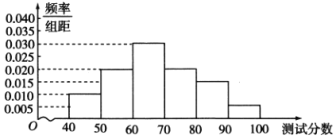
高中部的100名学生的成绩（单位：分）的频数分布表如下：
测试分数 |
|
|
|
|
|
频数 | 5 | 20 | 35 | 25 | 15 |
把成绩分为四个等级：60分以下为
级，60分（含60）到80分为
级，80分（含80）到90分为
级，90分（含90）以上为
级.
（1）根据已知条件完成下面的
列联表，据此资料你是否有99%的把握认为学生数学素养成绩“级”与“所在级部”有关？
不是 |
| 合计 | |
初中部 | |||
高中部 | |||
合计 |
注：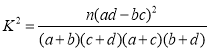
，其中
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（2）若这个学校共有9000名高中生，用频率估计概率，用样本估计总体，试估计这个学校的高中生的数学素养成绩为级的人数，并估计数学素养成绩的平均分（用组中值代表本组分数）；
（3）把初中部的级同学编号为
，
，
，
，
，高中部的级同学编号为
，
，
，
，
，从初中部级、高中部级中各选一名同学，求这两名同学的编号奇偶性相同的概率.
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费
和年销售量
（
）数据作了初步处理，得到下面的散点图及一些统计量的值．
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1.469 | 108.8 |
表中
，
（1）根据散点图判断，
与
哪一个适宜作为年销售量y关于年宣传费x的回归方类型？给出判断即可，不必说明理由
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；
（3）已知这种产品的年利润z与x、y的关系为
根据（2）的结果回答下列问题：
①年宣传费
时，年销售量及年利润的预报值是多少？
②年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据
，其回归线
的斜率和截距的最小二乘估计分别为：
，
．
【题目】已知
为等差数列，
，
，
分别是下表第一、二、三行中的某一个数，且，，中的任何两个数都不在下表的同一列．
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
请从①
，②
，③ 
的三个条件中选一个填入上表，使满足以上条件的数列存在；并在此存在的数列中，试解答下列两个问题
（1）求数列的通项公式；
（2）设数列
满足
，求数列的前n项和
．
