题目内容
已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
[解析] (1)∵f(x)=2x,
∴g(x)=f(2x)-f(x+2)=22x-2x+2.
∵f(x)的定义域是[0,3],
∴ 解得0≤x≤1.
解得0≤x≤1.
∴g(x)的定义域是[0,1].
(2)g(x)=(2x)2-4×2x
=(2x-2)2-4.
∵x∈[0,1],
∴2x∈[1,2].
∴当2x=1,即x=0时,g(x)取得最大值-3;
当2x=2,即x=1时,g(x)取得最小值-4.

练习册系列答案
相关题目
 D.f(x)=(
D.f(x)=(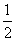 )x
)x (x2-3x)的单调递减区间是________.
(x2-3x)的单调递减区间是________.
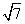 ,1,3} D.{-2-
,1,3} D.{-2- +tan
+tan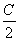 +
+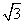 tan
tan
 ,且三角形有两解,则角A的取值范围是( )
,且三角形有两解,则角A的取值范围是( )