题目内容
已知P是直线 上的动点,PA、PB是圆
上的动点,PA、PB是圆 的两条切线,C是圆心,那么四边形PACB面积的最小值( )
的两条切线,C是圆心,那么四边形PACB面积的最小值( )
A. B.2
B.2 C.
C. D.2
D.2
C
解析试题分析:如图 ,所以四边形PACB面积的最小值就是
,所以四边形PACB面积的最小值就是 的最小值,而
的最小值,而 ,本题要求出最小的
,本题要求出最小的 的值,即为圆心C(1,1)到直线
的值,即为圆心C(1,1)到直线 的最短距离
的最短距离 ,所以
,所以 .即四边形PACB面积的最小值是
.即四边形PACB面积的最小值是 .所以选C.
.所以选C.
考点:1.点到直线的距离.2.切线的性质.3.转换的思想,把面积为题转化为线段的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知点P(3,4)和圆C:(x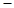 2)2+y2=4,A,B是圆C上两个动点,且|AB|=
2)2+y2=4,A,B是圆C上两个动点,且|AB|= ,则
,则 (O为坐标原点)的取值范围是( )
(O为坐标原点)的取值范围是( )
| A.[3,9] | B.[1,11] | C.[6,18] | D.[2,22] |
若直线 过圆
过圆 的圆心,则a的值为( )
的圆心,则a的值为( )
| A.-1 | B.1 | C.3 | D.-3 |
直线 被圆
被圆 截得的弦长为 ( )
截得的弦长为 ( )
A. | B. | C. | D.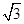 |
圆 的圆心坐标是( )
的圆心坐标是( )
| A.(2,3) | B.(-2,3) | C.(-2,-3) | D.(2,-3) |
若直线 与曲线
与曲线 有且只有两个公共点,则m的取值范围是( )
有且只有两个公共点,则m的取值范围是( )
A. | B. | C. | D. |
若直线 与曲线
与曲线 有交点,则( )
有交点,则( )
A. 有最大值 有最大值 ,最小值 ,最小值 | B. 有最大值 有最大值 ,最小值 ,最小值 |
C. 有最大值0,最小值 有最大值0,最小值  | D. 有最大值0,最小值 有最大值0,最小值 |
已知圆 :
: +
+ =1,圆
=1,圆 与圆
与圆 关于直线
关于直线 对称,则圆
对称,则圆 的方程为( )
的方程为( )
A. + + =1 =1 | B.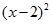 + + =1 =1 |
C. + + =1 =1 | D.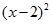 + + =1 =1 |
已知圆 在曲线
在曲线 的内部,则半径
的内部,则半径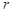 的范围是( )
的范围是( )
A.0<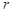 < < | B.0<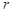 <2 <2 | C.0<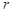 <2 <2 | D.0<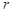 <4 <4 |