题目内容
已知二次函数f(x)=ax2+bx+c (a≠0)且满足f(-1)=0,对任意实数x,恒有f(x)-x≥0,并且当x∈(0,2)时,f(x)≤ .
.
(1)求f(1)的值;
(2)证明:a>0,c>0;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx (x∈R)是单调函数,求证:m≤0或m≥1.
 .
.(1)求f(1)的值;
(2)证明:a>0,c>0;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx (x∈R)是单调函数,求证:m≤0或m≥1.
(1)f(1)=1. (2)见解析 (3)见解析
(1)解 ∵对x∈R,f(x)-x≥0恒成立,
当x=1时,f(1)≥1,
又∵1∈(0,2),由已知得f(1)≤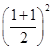 =1,
=1,
∴1≤f(1)≤1.∴f(1)=1.
(2)证明 ∵f(1)=1,∴a+b+c=1.
又∵a-b+c=0,∴b=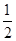 .∴a+c=
.∴a+c=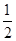 .
.
∵f(x)-x≥0对x∈R恒成立,
∴ax2-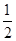 x+c≥0对x∈R恒成立.
x+c≥0对x∈R恒成立.
∴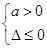 , ∴
, ∴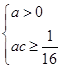 ∴c>0,故a>0,c>0.
∴c>0,故a>0,c>0.
(3)证明 ∵a+c=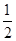 ,ac≥
,ac≥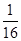 ,
,
由a>0,c>0及a+c≥2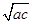 ,得ac≤
,得ac≤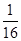 ,
,
∴ac=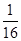 ,当且仅当a=c=
,当且仅当a=c=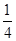 时,取“=”.
时,取“=”.
∴f(x)=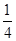 x2+
x2+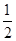 x+
x+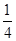 .
.
∴g(x)=f(x)-mx=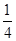 x2+
x2+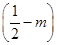 x+
x+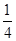
=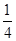 [x2+(2-4m)x+1].
[x2+(2-4m)x+1].
∵g(x)在[-1,1]上是单调函数,
∴2m-1≤-1或2m-1≥1.∴m≤0或m≥1.
当x=1时,f(1)≥1,
又∵1∈(0,2),由已知得f(1)≤
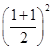 =1,
=1,∴1≤f(1)≤1.∴f(1)=1.
(2)证明 ∵f(1)=1,∴a+b+c=1.
又∵a-b+c=0,∴b=
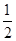 .∴a+c=
.∴a+c=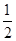 .
.∵f(x)-x≥0对x∈R恒成立,
∴ax2-
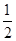 x+c≥0对x∈R恒成立.
x+c≥0对x∈R恒成立.∴
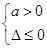 , ∴
, ∴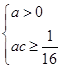 ∴c>0,故a>0,c>0.
∴c>0,故a>0,c>0.(3)证明 ∵a+c=
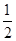 ,ac≥
,ac≥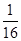 ,
,由a>0,c>0及a+c≥2
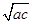 ,得ac≤
,得ac≤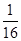 ,
,∴ac=
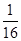 ,当且仅当a=c=
,当且仅当a=c=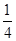 时,取“=”.
时,取“=”.∴f(x)=
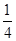 x2+
x2+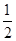 x+
x+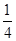 .
.∴g(x)=f(x)-mx=
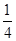 x2+
x2+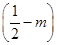 x+
x+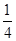
=
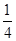 [x2+(2-4m)x+1].
[x2+(2-4m)x+1].∵g(x)在[-1,1]上是单调函数,
∴2m-1≤-1或2m-1≥1.∴m≤0或m≥1.

练习册系列答案
相关题目

 ,求
,求 的最大值与最小值;
的最大值与最小值;  的最大值与最小值;
的最大值与最小值; 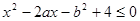 恰有一解,则
恰有一解,则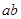 的最大值为______.
的最大值为______. 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点 、
、 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为 .
. ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求 的取值范围.
的取值范围.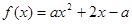 满足
满足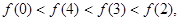 则
则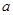 的取值范围为_____
的取值范围为_____ .设
.设 ,
, (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记 的最小值为A,
的最小值为A, 的最大值为B,则
的最大值为B,则 ( )
( )


 (x
(x -2x+3)有以下4个结论:其中正确的有 .
-2x+3)有以下4个结论:其中正确的有 .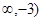
 ; ② 递增区间为
; ② 递增区间为 ;
; 轴的上方.
轴的上方.