题目内容
若f(x)对一切实数x都有f(x+8)=-f(-2-x),且x>3时,f(x)=x2-7x+4.
(1)求f(x)在R上的解析式;
(2)若φ(x)=2lnx-x2+(5-
)x,h(x)=φ(x)-f(x),当x<3时,求h(x)的单调递增区间.
(1)求f(x)在R上的解析式;
(2)若φ(x)=2lnx-x2+(5-
| 1 | a |
分析:(1)根据f(x+8)=-f(-2-x),可得f(x)=-f(6-x),当x=3时,f(3)=0,当x<3时,6-x>3,f(x)=-f(6-x)=-[(6-x)2-7(6-x)+4]=-x2+5x+2,从而可得函数的解析式;
(2)当x<3时,h(x)=2lnx-x2+(5-
)x+x2-5x-2=2lnx-
x-2,求导函数可得h′(x)=
-
=
(a≠0),定义域为(0,3),利用导数的正负可得结论.
(2)当x<3时,h(x)=2lnx-x2+(5-
| 1 |
| a |
| 1 |
| a |
| 2 |
| x |
| 1 |
| a |
| 2a-x |
| ax |
解答:解:(1)f(x+8)=-f(-2-x),∴以x+8代x可得f(x)=-f(6-x),
当x=3时,f(3)=-f(3),∴f(3)=0
当x<3时,6-x>3,∴f(x)=-f(6-x)=-[(6-x)2-7(6-x)+4]=-x2+5x+2,
综上:f(x)=
(2)当x<3时,h(x)=2lnx-x2+(5-
)x+x2-5x-2=2lnx-
x-2,
求导函数可得h′(x)=
-
=
(a≠0),定义域为(0,3)
当a<0时,h′(x)>0恒成立,
当0<a≤
时,由h′(x)>0得0<x<2a;当a>
时,x∈(0,3),恒有h′(x)>0
综上:当a<0或a>
时,h(x)的增区间为(0,3);当0<a≤
时,h(x)的增区间为(0,2a).
当x=3时,f(3)=-f(3),∴f(3)=0
当x<3时,6-x>3,∴f(x)=-f(6-x)=-[(6-x)2-7(6-x)+4]=-x2+5x+2,
综上:f(x)=
|
(2)当x<3时,h(x)=2lnx-x2+(5-
| 1 |
| a |
| 1 |
| a |
求导函数可得h′(x)=
| 2 |
| x |
| 1 |
| a |
| 2a-x |
| ax |
当a<0时,h′(x)>0恒成立,
当0<a≤
| 3 |
| 2 |
| 3 |
| 2 |
综上:当a<0或a>
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了函数的定义、性质、导数法求单调区间以及分类讨论的思想.

练习册系列答案
相关题目
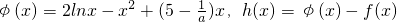 ,当x<3时,求h(x)的单调递增区间.
,当x<3时,求h(x)的单调递增区间.