题目内容
设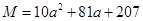 ,
,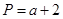 ,Q=
,Q=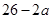 ;若将
;若将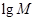 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列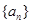 的前三项.
的前三项.
(1)试比较M、P、Q的大小;
(2)求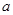 的值及
的值及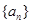 的通项;
的通项;
(3)记函数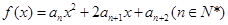 的图象在
的图象在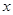 轴上截得的线段长为
轴上截得的线段长为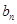 ,
,
设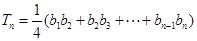
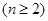 ,求
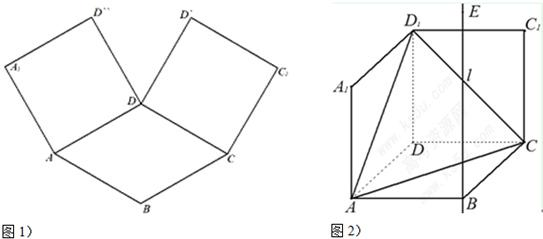
,求 ,并证明
,并证明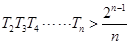 .
.
【答案】
(1)当 时:
时: ;当
;当 时:
时:  ;当
;当 时:
时: ;
;
(2)当 时:
时: ;当
;当 时:无解.
时:无解.
【解析】
试题分析:(1)两两之间作差比较大小;(2)根据第(1)问的结果结合等差数列项的关系求解;(3)先求出线段长 ,再表示出
,再表示出 ,通过裂项相消化简求值
,通过裂项相消化简求值 ,再结合放缩法求范围
,再结合放缩法求范围
试题解析:(1)由 得
得 2分
2分
 3分
3分
 4分
4分
 ,
,
又 当
当 时,
时, ,
,
当 时,即
时,即 ,则
,则 5分
5分
当 时,
时, ,则
,则
当 时,
时, ,则
,则
(2)当 时,
时,
 即
即


解得 ,从而
,从而 7分
7分
当 时,
时,
 即
即

 ,
,  无解. 8分
无解. 8分
(3)设 与
与 轴交点为
轴交点为
 ,
,
 当
当 =0时有
=0时有
 9分
9分

又 ,
,


 11分
11分

 14分
14分
考点:1.作差比较大小;2.分类讨论思想;3.等差数列通项;4.裂项相消求和;5.放缩法应用.

练习册系列答案
相关题目
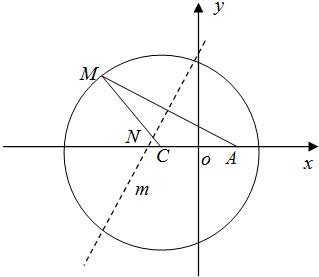 如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.
如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E. 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).

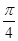 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围; 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有 且
且 的菱形,
的菱形, 和
和 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使 与
与 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设 (图2)。
(图2)。

 ,求
,求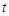 的取值范围;
的取值范围; 上是否存在点
上是否存在点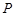 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
