题目内容
已知f(x)=cos2x-4sinxcosx-3sin2x。
(1)若0≤x≤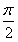 ,求f(x)的最大值和最小值;
,求f(x)的最大值和最小值;
(2)求f(x)的增区间;
(3)f(x)的图象是由y=cosx的图象经过怎样的变换得到的?
(1)若0≤x≤
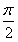 ,求f(x)的最大值和最小值;
,求f(x)的最大值和最小值;(2)求f(x)的增区间;
(3)f(x)的图象是由y=cosx的图象经过怎样的变换得到的?
解:(1)利用二倍角余弦公式的变形公式,有
y=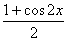 -2sin2x-3·
-2sin2x-3·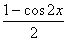
=2(cos2x-sin2x)-1
=2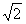 (cos2xcos
(cos2xcos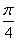 -sin2xsin
-sin2xsin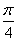 )-1
)-1
=2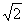 cos(2x+
cos(2x+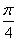 )-1,
)-1,
∵0≤x≤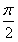 ,
,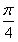 ≤2x+
≤2x+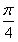 ≤
≤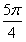 ,
,
∴cos(2x+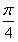 )在[0,
)在[0,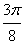 )上是减函数,
)上是减函数,
故当x=0时,有最大值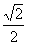 ;当x=
;当x=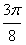 时,有最小值-1;
时,有最小值-1;
cos(2x+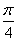 )在[
)在[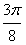 ,
,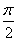 ]上是增函数,故当x=
]上是增函数,故当x=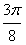 时,有最小值-1;当x=
时,有最小值-1;当x=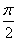 时,有最大值
时,有最大值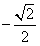 ;
;
综上所述,当x=0时,ymax=1;当x=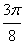 时,ymin=-2
时,ymin=-2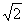 -1。
-1。
(2)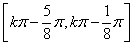 ;
;
(3)将y=cosx的图象上的所有点向左平移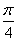 个单位,然后把曲线上所有点的横坐标缩短到原来的
个单位,然后把曲线上所有点的横坐标缩短到原来的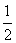 ,再把曲线上各点的纵坐标变为原来的
,再把曲线上各点的纵坐标变为原来的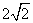 倍,最后将曲线上的所有点向下平移1个单位长度,得到2
倍,最后将曲线上的所有点向下平移1个单位长度,得到2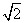
cos(2x+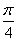 )-1的图象。
)-1的图象。
y=
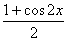 -2sin2x-3·
-2sin2x-3·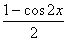
=2(cos2x-sin2x)-1
=2
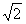 (cos2xcos
(cos2xcos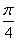 -sin2xsin
-sin2xsin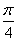 )-1
)-1=2
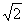 cos(2x+
cos(2x+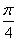 )-1,
)-1,∵0≤x≤
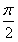 ,
,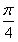 ≤2x+
≤2x+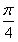 ≤
≤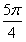 ,
,∴cos(2x+
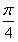 )在[0,
)在[0,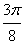 )上是减函数,
)上是减函数, 故当x=0时,有最大值
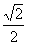 ;当x=
;当x=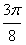 时,有最小值-1;
时,有最小值-1;cos(2x+
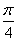 )在[
)在[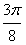 ,
,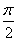 ]上是增函数,故当x=
]上是增函数,故当x=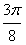 时,有最小值-1;当x=
时,有最小值-1;当x=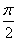 时,有最大值
时,有最大值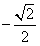 ;
;综上所述,当x=0时,ymax=1;当x=
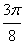 时,ymin=-2
时,ymin=-2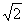 -1。
-1。 (2)
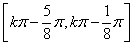 ;
;(3)将y=cosx的图象上的所有点向左平移
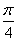 个单位,然后把曲线上所有点的横坐标缩短到原来的
个单位,然后把曲线上所有点的横坐标缩短到原来的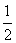 ,再把曲线上各点的纵坐标变为原来的
,再把曲线上各点的纵坐标变为原来的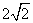 倍,最后将曲线上的所有点向下平移1个单位长度,得到2
倍,最后将曲线上的所有点向下平移1个单位长度,得到2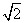
cos(2x+
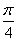 )-1的图象。
)-1的图象。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)=cos(ωx+
),(ω>0)的图象与y=1的图象的两相邻交点间的距离为π,要得到y=f(x)的图象,只须把y=sinωx的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知f(x)=
,则f(
)+f(-
)的值为( )
|
| 4 |
| 3 |
| 4 |
| 3 |
| A、-2 | B、-1 | C、1 | D、2 |