题目内容
设数列{an}是以 展开式的常数项为首项,并且以椭圆3x2+4y2-6x-9=0的离心率为公比的无穷等比数列,
展开式的常数项为首项,并且以椭圆3x2+4y2-6x-9=0的离心率为公比的无穷等比数列, 为 .
为 .
【答案】分析:利用二项式展开式的通项公式求出a1=-20,再求出椭圆的离心率为 ,求出此等比数列的前n项和,利用数列极限的运算法则求出结果.
,求出此等比数列的前n项和,利用数列极限的运算法则求出结果.
解答:解:∵ 展开式的通项Tr+1=C6r
展开式的通项Tr+1=C6r 
 =
= ,
,
令r=3 可得常数项为-20,即a1=-20.
椭圆3x2+4y2-6x-9=0即 ,离心率为
,离心率为 ,故数列{an} 的公比的等于
,故数列{an} 的公比的等于 .
.
此等比数列的前n项和为 a1+a2+…+an=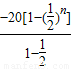 =-40(1-
=-40(1- ).
).
∴ =
= =-40,
=-40,
故答案为:-40.
点评:本题考查求二项式展开式的某项的系数,椭圆的简单性质,等比数列的前n项和公式,以及数列极限的运算法则,求出 a1+a2+…+an=-40(1- ),是解题的关键和难点.
),是解题的关键和难点.
 ,求出此等比数列的前n项和,利用数列极限的运算法则求出结果.
,求出此等比数列的前n项和,利用数列极限的运算法则求出结果.解答:解:∵
 展开式的通项Tr+1=C6r
展开式的通项Tr+1=C6r 
 =
= ,
,令r=3 可得常数项为-20,即a1=-20.
椭圆3x2+4y2-6x-9=0即
 ,离心率为
,离心率为 ,故数列{an} 的公比的等于
,故数列{an} 的公比的等于 .
.此等比数列的前n项和为 a1+a2+…+an=
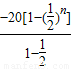 =-40(1-
=-40(1- ).
).∴
 =
= =-40,
=-40,故答案为:-40.
点评:本题考查求二项式展开式的某项的系数,椭圆的简单性质,等比数列的前n项和公式,以及数列极限的运算法则,求出 a1+a2+…+an=-40(1-
 ),是解题的关键和难点.
),是解题的关键和难点. 
练习册系列答案
相关题目
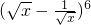 展开式的常数项为首项,并且以椭圆3x2+4y2-6x-9=0的离心率为公比的无穷等比数列,
展开式的常数项为首项,并且以椭圆3x2+4y2-6x-9=0的离心率为公比的无穷等比数列,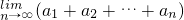 为________.
为________.