题目内容
抛物线y2=4x经过焦点的弦的中点的轨迹方程是
- A.y2=x-1
- B.y2=2(x-1)
- C.

- D.y2=2x-1
B
分析:先根据抛物线方程求得焦点坐标,进而设出过焦点弦的直线方程,与抛物线方程联立消去y,根据韦达定理表示出x1+x2,进而根据直线方程求得y1+y2,进而求得焦点弦的中点的坐标的表达式,消去参数k,则焦点弦的中点轨迹方程可得.
解答:由题知抛物线焦点为(1,0)
设焦点弦方程为y=k(x-1)
代入抛物线方程得所以k2x2-(2k2+4)x+k2=0
由韦达定理:
x1+x2=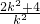
所以中点横坐标:x= =
=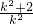
代入直线方程
中点纵坐标:
y=k(x-1)= .即中点为(
.即中点为(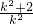 ,
, )
)
消参数k,得其方程为
y2=2x-2
故选B.
点评:本题主要考查了抛物线的简单性质.考查了学生对抛物线基本性质的熟练掌握.
分析:先根据抛物线方程求得焦点坐标,进而设出过焦点弦的直线方程,与抛物线方程联立消去y,根据韦达定理表示出x1+x2,进而根据直线方程求得y1+y2,进而求得焦点弦的中点的坐标的表达式,消去参数k,则焦点弦的中点轨迹方程可得.
解答:由题知抛物线焦点为(1,0)
设焦点弦方程为y=k(x-1)
代入抛物线方程得所以k2x2-(2k2+4)x+k2=0
由韦达定理:
x1+x2=
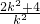
所以中点横坐标:x=
 =
=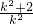
代入直线方程
中点纵坐标:
y=k(x-1)=
 .即中点为(
.即中点为(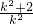 ,
, )
)消参数k,得其方程为
y2=2x-2
故选B.
点评:本题主要考查了抛物线的简单性质.考查了学生对抛物线基本性质的熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线y2=4x经过焦点的弦的中点的轨迹方程是( )
| A、y2=x-1 | ||
| B、y2=2(x-1) | ||
C、y2=x-
| ||
| D、y2=2x-1 |
