题目内容
14.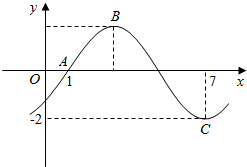 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.(1)写出函数f(x)的最小正周期及其单调递减区间;
(2)求f(x)的解析式;
(3)若将函数f(x)的图象平移Φ个单位,得到一个偶函数的图象,求|Φ|的最小值;
(4)求函数y=f(x-3)+f(2x+7)(x∈[0,2])的值域.
分析 (1)由正弦函数图象的特点可得周期T,结合图象可得函数的单调递减区间;
(2)由周期性可得ω=$\frac{π}{4}$,可得A=2,代入点(7,-2)可得φ值,可得解析式;
(3)由函数图象变换和偶函数可得$\frac{π}{4}$Φ-$\frac{π}{4}$=kπ+$\frac{π}{2}$,解得Φ=4k+3,k∈Z,给k取值可得|Φ|的最小值;
(4)代入化简可得y=-4sin2$\frac{π}{4}$x-2sin$\frac{π}{4}$x+2,由二次函数区间的值域可得.
解答 解:(1)由正弦函数图象的特点可知周期T满足$\frac{3}{4}$T=7-1,
解得周期T=8,结合图象可得函数的单调递减区间为[8k+3,8k+7],k∈Z;
(2)由(1)可得$\frac{2π}{ω}$=8,解得ω=$\frac{π}{4}$,A=2,故f(x)=2sin($\frac{π}{4}$x+φ),
代入点(7,-2)可得-2=2sin($\frac{π}{4}$×7+φ),
结合|φ|<$\frac{π}{2}$可得φ=-$\frac{π}{4}$,故函数解析式为f(x)=2sin($\frac{π}{4}$x-$\frac{π}{4}$);
(3)将函数f(x)=2sin($\frac{π}{4}$x-$\frac{π}{4}$)的图象平移Φ个单位,
得到函数的解析式为y=2sin[$\frac{π}{4}$(x+Φ)-$\frac{π}{4}$)]=2sin($\frac{π}{4}$x+$\frac{π}{4}$Φ-$\frac{π}{4}$),
由偶函数可得$\frac{π}{4}$Φ-$\frac{π}{4}$=kπ+$\frac{π}{2}$,解得Φ=4k+3,k∈Z,
取k=-1时,可得Φ=-1,此时|Φ|取最小值1;
(4)函数y=f(x-3)+f(2x+7)
=2sin[$\frac{π}{4}$(x-3)-$\frac{π}{4}$)]+2sin[$\frac{π}{4}$(2x+7)-$\frac{π}{4}$)]
=2sin($\frac{π}{4}$x-π)+2sin($\frac{π}{2}$x-$\frac{3π}{2}$)
=-2sin$\frac{π}{4}$x+2cos$\frac{π}{2}$x
=-2sin$\frac{π}{4}$x+2(1-2sin2$\frac{π}{4}$x)
=-4sin2$\frac{π}{4}$x-2sin$\frac{π}{4}$x+2,
∵x∈[0,2],∴$\frac{π}{4}$x∈[0,$\frac{π}{2}$],
∴sin$\frac{π}{4}$x∈[0,1],
由二次函数可知当sin$\frac{π}{4}$x=0时,函数取最大值2,
当sin$\frac{π}{4}$x=1时,函数取最小值-4,
故函数的值域为:[-4,2].
点评 本题考查正弦函数的图象,涉及函数图象的变换和二次函数区间的最值,属中档题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案| A. | $\sqrt{3}-1$ | B. | $2\sqrt{3}+2$ | C. | $\sqrt{3}+1$ | D. | $2\sqrt{3}-2$ |
| 商店名称 | A | B | C | D | E |
| 销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(2)若商店F此月的销售额为1亿1千万元,试用(1)中求得的回归方程,估测其利润.(精确到百万元)