题目内容
12.函数y=$\sqrt{-2sinx}$的定义域是[π+2kπ,2π+2kπ],(k∈Z),单调递减区间是[2k$π-\frac{π}{2}$,2kπ],(k∈Z).分析 由-2sinx≥0,化为sinx≤0,解出即可得出定义域.函数y=$\sqrt{-2sinx}$的单调递减区间,即求函数 y=sinx的单调递增区间.
解答 解:由-2sinx≥0,化为sinx≤0,解得π+2kπ≤x≤2π+2kπ,k∈Z,
∴y=$\sqrt{-2sinx}$的定义域是[π+2kπ,2π+2kπ],(k∈Z).
函数y=$\sqrt{-2sinx}$的单调递减区间是[2k$π-\frac{π}{2}$,2kπ],(k∈Z).
故答案分别为:[π+2kπ,2π+2kπ],(k∈Z);[2k$π-\frac{π}{2}$,2kπ],(k∈Z).
点评 本题考查了三角函数的定义域与单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
3.在以A(2,1),B(4,2),C(8,5)为顶点的三角形中,BC边上的高等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | 2 |
 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,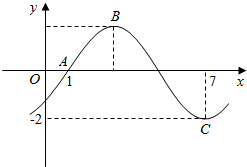 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.