题目内容
19.若a,b,c>0,且$a(a+b+c)+bc=4+2\sqrt{3}$,则2a+b+c的最小值为( )| A. | $\sqrt{3}-1$ | B. | $2\sqrt{3}+2$ | C. | $\sqrt{3}+1$ | D. | $2\sqrt{3}-2$ |
分析 由题意知a(a+b+c)+bc=(a+c)(a+b)=4+2$\sqrt{3}$,所以2a+b+c=(a+b)+(a+c)≥2$\sqrt{(a+b)(a+c)}$=2$\sqrt{4+2\sqrt{3}}$=2$\sqrt{3}$+2,即可求出2a+b+c的最小值.
解答 解:a(a+b+c)+bc=a(a+b)+ac+bc
=a(a+b)+c(a+b)=(a+c)(a+b)=4+2$\sqrt{3}$.
2a+b+c=(a+b)+(a+c)
≥2$\sqrt{(a+b)(a+c)}$=2$\sqrt{4+2\sqrt{3}}$=2$\sqrt{3}$+2,
所以,2a+b+c的最小值为2$\sqrt{3}$+2.
故选:B.
点评 本题考查不等式的基本性质和应用:求最值,解题时注意变形,运用因式分解和整体思想,属于中档题.

练习册系列答案
相关题目
10.设函数f(x)=x2-ax+a+3,g(x)=ax-2a.
(1)当x>1时,方程f(x)=0有解,求a的取值范;
(2)若存在x0∈R,使得f(x0)<0与g(x0)<0同时成立,求a的取值范围.
(1)当x>1时,方程f(x)=0有解,求a的取值范;
(2)若存在x0∈R,使得f(x0)<0与g(x0)<0同时成立,求a的取值范围.
8.下列函数在(-∞,0)∪(0,+∞)上既是偶函数,又在(0,+∞)上单调递增的是( )
| A. | y=-x2 | B. | y=x-1 | C. | y=log2|x| | D. | y=-2x |
 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,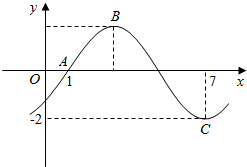 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.