题目内容
(满分12分)已知 对一切实数
对一切实数 都有
都有 ,当
,当 >0时,
>0时, <0.
<0.
(1)证明 为
为 上的减函数;(2)解不等式
上的减函数;(2)解不等式 <4
<4
(1)略;(2) 或
或
【解析】
试题分析:(1)由题根据所给抽象函数满足条件,通过变换 可以证明函数为减函数;(2)首先证明函数在R上为减函数,结合
可以证明函数为减函数;(2)首先证明函数在R上为减函数,结合 ,得到x的取值范围.
,得到x的取值范围.
试题解析:(1)证明:设 则
则 其中
其中 ,
,
∴

∵ ∴
∴
∴
∴ 在R上减函数 6分
在R上减函数 6分
(2)【解析】
依题意有
∴不等式可化为
即 ,
,
因为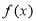 是R上的减函数∴
是R上的减函数∴ ,
, 或
或
所以不等式的解集为 或
或 12分
12分
考点:抽象函数的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,则
的图象,则 .
. 满足
满足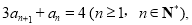 且
且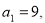 其前
其前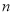 项之和为
项之和为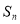 ,则满足不等式
,则满足不等式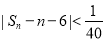 成立的
成立的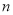 的最小值是
的最小值是 ,
, 满足约束条件
满足约束条件 则
则 的最大值是 .
的最大值是 .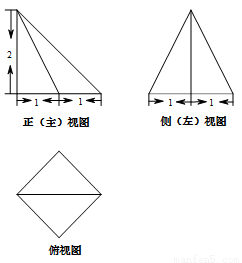
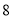 B.
B. C.
C.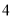 D.
D.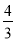
 的解集为
的解集为 ,则实数
,则实数 的取值范围是 _______.
的取值范围是 _______.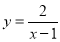 的定义域是(-∞,1)∪[2,5),则其值域是( )
的定义域是(-∞,1)∪[2,5),则其值域是( ) 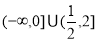 B.(-∞,2]
B.(-∞,2]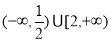 D.(0,+∞)
D.(0,+∞) .
. 有两个不同的实数根,则实数
有两个不同的实数根,则实数 的取值范围为_______.
的取值范围为_______.