题目内容
15．在△ABC中，a，b，c分别是内角A，B，C的对边，若A=$\frac{2π}{3}$，b=$\sqrt{2}$，△ABC的面积为$\sqrt{3}$，则a的值为$\sqrt{14}$．分析 由已知利用三角形面积公式可求c，利用余弦定理即可解得a的值．
解答 解：∵由S△ABC=$\frac{1}{2}$bcsinA，可得：$\frac{1}{2}×\sqrt{2}×c×sin\frac{2π}{3}$=$\sqrt{3}$，解得：c=2$\sqrt{2}$，
∴a2=b2+c2-2bccosA=2$+8-2×\sqrt{2}×2\sqrt{2}×（-\frac{1}{2}）$=14，
∴a=$\sqrt{14}$．
故答案为：$\sqrt{14}$．
点评 本题主要考查了三角形面积公式，余弦定理在解三角形中的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
3．
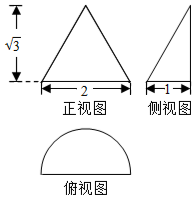已知某几何体的三视图如图所示，则该几何体的表面积为（ ）
已知某几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | $\frac{5π}{2}+\sqrt{3}$ | B． | $\frac{3π}{2}+2$ | C． | $\frac{π}{2}+\sqrt{3}$ | D． | $\frac{3π}{2}+\sqrt{3}$ |
20．
某中学共有1000名学生参加考试，成绩如表：
（1）为了了解同学们的具体情况，学校将采取分层抽样的方法，抽取100名同学进行问卷调查，甲同学在本次测试中成绩为95分，求他被抽中的概率．
（2）本次数学成绩的优秀成绩为110分，试估计该中学达到优秀线的人数．
（3）作出频率分布直方图，并据此估计该校本次考试的平均分（用同一组中得到数据用该组区间的中点值作代表）
某中学共有1000名学生参加考试，成绩如表：| 成绩分组 | [0，30） | [30，60） | [60，90） | [90，120） | [120，150） |
| 人 数 | 60 | 90 | 300 | x | 160 |
（2）本次数学成绩的优秀成绩为110分，试估计该中学达到优秀线的人数．
（3）作出频率分布直方图，并据此估计该校本次考试的平均分（用同一组中得到数据用该组区间的中点值作代表）
4．已知$tan（α+\frac{π}{4}）=2$，则tan2α=（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{3}{5}$ | C． | $-\frac{3}{4}$ | D． | $-\frac{3}{5}$ |