题目内容
已知抛物线y2=2x,设A,B是抛物线上不重合的两点,且| OA |
| OB |
| OM |
| OA |
| OB |
(1)若|
| OA |
| OB |
(2)求动点M的轨迹方程.
分析:(1)若|
|=|
|,由抛物线的对称性知,AB垂直于横轴,可设直线AB的方程是x=b,用b表示出两点A,B的坐标,再由
⊥
建立方程求出b即可,利用向量的坐标运算,求出向量OM的坐标既得点M的坐标.
(2)设出直线AB的方程y=kx+b,与抛物线的方程联立,利用
⊥
,找出两参数的关系,用参数表示出两点A,B的横坐标的和与纵坐标的和,即得出点M的坐标的参数方程,消去参数即得点M的轨迹方程.
| OA |
| OB |
| OA |
| OB |
(2)设出直线AB的方程y=kx+b,与抛物线的方程联立,利用
| OA |
| OB |
解答:解:(1)若|
|=|
|,由抛物线的对称性知,AB垂直于横轴,可设直线AB的方程是x=b,可解得A,B两点的坐标分别为(b,
),(b,-
),则
=(b,
)
=(b,-
),有
⊥
得b2-2b=0,得b=0(舍),b=2,故,B两点的坐标分别为(2,2),(2,-2)
又
=
+
=(4,0),故点M的坐标为(4,0),
(2)当斜率不存在时,由(1)知点M的坐标为(4,0),
当斜率存在时,可设过两点A,B的直线方程为x=ny+m代入抛物线y2=2x得y2=2ny+2m,即y2-2ny-2m=0,令A(x1,y1),B(x2,y2)
则有y1y2=-2m,y1+y2=2n,
故有x1x2=(ny1+m)(ny2+m)=n2y1y2+nm(y1+y2)+m2=-2mn2+2mn2+m2=m2,
x1+x2=n(y1+y2)+2m=2n2+2m
∵
⊥
,∴x1x2+y1y2=0,∴-2m+m2=0,得m=2或m=0(舍)
∵
=
+
=(x1+x2,y1+y2)=(2n2+2m,2n)=(2n2+4,2n),令M(x,y),则有
,消去参数得x=
+4,即y2=2x-8
验证知点M的坐标为(4,0)符合y2=2x-8
故动点M的轨迹方程是y2=2x-8
| OA |
| OB |
| 2b |
| 2b |
| OA |
| 2b |
| OB |
| 2b |
| OA |
| OB |
又
| OM |
| OA |
| OB |
(2)当斜率不存在时,由(1)知点M的坐标为(4,0),
当斜率存在时,可设过两点A,B的直线方程为x=ny+m代入抛物线y2=2x得y2=2ny+2m,即y2-2ny-2m=0,令A(x1,y1),B(x2,y2)
则有y1y2=-2m,y1+y2=2n,
故有x1x2=(ny1+m)(ny2+m)=n2y1y2+nm(y1+y2)+m2=-2mn2+2mn2+m2=m2,
x1+x2=n(y1+y2)+2m=2n2+2m
∵
| OA |
| OB |
∵
| OM |
| OA |
| OB |
|
| y2 |
| 2 |
验证知点M的坐标为(4,0)符合y2=2x-8
故动点M的轨迹方程是y2=2x-8
点评:本题考查向量在几何中的应用,考查了由抛物线的简单性质,以及根据抛物线的两点之间的位置关系求动点的轨迹方程,求解本题的关键是厘清题设中所给的条件,以及向量的坐标运算,数量积与垂直的关系,向量垂直时坐标之间的关系,本题的难点在于设出过两点AB的直线方程与抛物线联立寻求抛物线上两点的坐标之间的参数表示,解题过程中要联想到所解出的坐标方程与题设中位置关系的联系.解题最后所得的点M的参数方程,由于近几年大多教材都删去了参数方程这一部分的知识,故在做此题时,没有学过参数方程的同学解出
就不用再往下化简了.
|

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
已知抛物线y2=2x,设点A的坐标为(
,0),则抛物线上距点A最近的点P的坐标为( )
| 2 |
| 3 |
| A、(0,0) |
| B、(0,1) |
| C、(1,0) |
| D、(-2,0) |
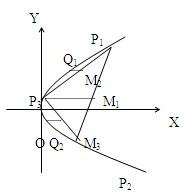 已知抛物线y2=2x.
已知抛物线y2=2x.