题目内容
已知数列{![]() }满足
}满足![]() ,且
,且![]() .
.
(1)若![]() =1,求数列{
=1,求数列{![]() }的通项公式;
}的通项公式;
(2)是否存在实数![]() ,使不等式
,使不等式![]() ≥2(
≥2(![]() )恒成立?若存在,求出
)恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)当一3≤![]() <1时,证明:
<1时,证明:![]() .
.
解:(1)∵![]() =1,∴
=1,∴![]() .
.
∵ ![]() ,显然
,显然![]() ≠0,
≠0,
∴![]() .
.
∴{![]() }是以2为首项、2为公比的等比数列,
}是以2为首项、2为公比的等比数列,
∴![]() =2n.
=2n.
(2)若![]() ≥2,
≥2,
则![]() ≥-
≥-![]() .
.
记![]() ,
,
可得![]() max=-3.
max=-3.
∴![]() <一3.故存在
<一3.故存在![]() ≥一3,使
≥一3,使![]() ≥2恒成立.
≥2恒成立.
(3)∵![]() =2
=2![]() +
+![]()
又一3≤![]() <1,由(2)知
<1,由(2)知![]() ≥2.
≥2.
∴![]() <0.∴
<0.∴![]() <2
<2![]()
∴2≤![]() <2
<2![]() <22
<22![]() <…<2n―1
<…<2n―1![]() 1=2n (
1=2n (![]() ∈N*)∴
∈N*)∴![]()
∴![]() =
=
![]()

练习册系列答案
相关题目
 满足
满足 ,且
,且 (
( )
) ,
, ,
, (2)由(1)猜想
(2)由(1)猜想 ;
; 满足
满足 ,且
,且 (
( )。
)。 、
、 、
、 的值;
的值; 满足
满足 ,且
,且 (n
(n 2且n∈N*).
2且n∈N*). 的通项公式;(5分)
的通项公式;(5分) ,求
,求 ,并证明:
,并证明: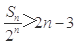 .(7分)
.(7分) 满足
满足 ,且
,且 ,且
,且 ,则数列
,则数列
 B.
B. C.
C. D.
D.