Question

已知函数g（x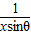）=+lnx在[1，+∞）上为增函数，其中θ∈（0，π），
（1）求θ的取值集合；
（2）f（x）=mx-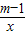-lnx（m∈R），若y=f（x）-g（x）在[1，+∞）上为单调函数，求m的取值范围．

Answer 1

【答案】分析：（1）由原函数为[1，+∞）上为增函数，得其导函数在[1，+∞）上恒成立，通分整理后根据θ的范围得到xsinθ-1≥0在[1，+∞）上恒成立，由正弦函数的值域结合角的范围可得答案；
（2）求出函数y=f（x）-g（x）的解析式，利用函数在[1，+∞）上为单调函数，得其导函数在[1，+∞）上大于等于0或小于等于0恒成立，分离变量后利用函数的单调性可求范围．
解答：解：（1）由g（x）=+lnx在[1，+∞）上为增函数，得
在[1，+∞）上恒成立，即，
∵θ∈（0，π），∴sinθ＞0，故xsinθ-1≥0在[1，+∞）上恒成立，
只需1•sinθ-1≥0，即sinθ≥1，结合θ∈（0，π），得．
所以，θ的取值集合为{}；
（2）由（1）得，f（x）-g（x）=mx-，，
由于f（x）-g（x）在其定义域内为单调函数，
则mx²-2x+m≥0或mx²-2x+m≤0在[1，+∞）上恒成立，
即或在[1，+∞）上恒成立，
故m≥1或m≤0．
综上，m的取值范围是（-∞，0]∪[1，+∞）．
点评：本题主要考查函数的单调性与其导函数的正负之间的关系，考查了数学转化思想方法和分离参数法，训练了利用函数的单调性求函数的最值，是中档题．