题目内容
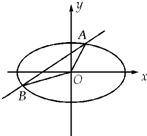 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
(1)求椭圆C的方程.
(2)试判断|OA|2+|OB|2是否为定值?若是,求出这个值;若不是,请说明理由?
(3)求S的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆C:
+
=1(a>b>0)的长轴是短轴的两倍,点A(
,
)在椭圆上,建立方程,求出几何量,即可求椭圆C的方程.
(2)设直线l的方程为y=kx+m,代入椭圆方程,消去y,根据k1、k、k2恰好构成等比数列,求出k,进而表示出|OA|2+|OB|2,即可得出结论;
(3)表示出△ABO的面积,利用基本不等式,即可求S的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
(2)设直线l的方程为y=kx+m,代入椭圆方程,消去y,根据k1、k、k2恰好构成等比数列,求出k,进而表示出|OA|2+|OB|2,即可得出结论;
(3)表示出△ABO的面积,利用基本不等式,即可求S的最大值.
解答:
解:(1)由题意可知a=2b且
+
=1,
∴a=2,b=1,…2分
∴椭圆的方程为
+y2=1;
(2)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),
由直线l的方程代入椭圆方程,消去y得:(1+4k2)x2+8kmx+4m2-4=0,
∴x1+x2=-
,x1x2=
且△=16(1+4k2-m2)>0,
∵k1、k、k2恰好构成等比数列.
∴k2=k1k2=
∴-4k2m2+m2=0,
∴k=±
,
此时△=16(2-m2)>0,即m∈(-
,
)
∴x1+x2=±2m,x1x2=2m2-2
∴|OA|2+|OB|2=x12+y12+x22+y22=
[(x1+x2)2-2x1x2]+2=5,
∴|OA|2+|OB|2是定值为5.…
(3)S=
|AB|d=
|x1-x2|•
=
|m|
=
≤
=1,
当且仅当m=±1时,S的最大值为1.
| 3 |
| a2 |
| 1 |
| 4b2 |
∴a=2,b=1,…2分
∴椭圆的方程为
| x2 |
| 4 |
(2)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),
由直线l的方程代入椭圆方程,消去y得:(1+4k2)x2+8kmx+4m2-4=0,
∴x1+x2=-
| 8km |
| 1+4k2 |
| 4m2-4 |
| 1+4k2 |
∵k1、k、k2恰好构成等比数列.
∴k2=k1k2=
| (kx1+m)(kx2+m) |
| x1x2 |
∴-4k2m2+m2=0,
∴k=±
| 1 |
| 2 |
此时△=16(2-m2)>0,即m∈(-
| 2 |
| 2 |
∴x1+x2=±2m,x1x2=2m2-2
∴|OA|2+|OB|2=x12+y12+x22+y22=
| 3 |
| 4 |
∴|OA|2+|OB|2是定值为5.…
(3)S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
| |m| | ||
|
| 1 |
| 2 |
| 4m2-(8m2-8) |
=
| (2-m2)m2 |
(
|
当且仅当m=±1时,S的最大值为1.
点评:本题考查椭圆的标准方程,直线与椭圆的位置关系,等比数列的性质,基本不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列四个结论:
(1)两条直线都和同一个平面平行,则这两条直线平行;
(2)两条直线没有公共点,则这两条直线平行;
(3)两条直线都和第三条直线垂直,则这两条直线平行;
其中正确的命题个数为( )
(1)两条直线都和同一个平面平行,则这两条直线平行;
(2)两条直线没有公共点,则这两条直线平行;
(3)两条直线都和第三条直线垂直,则这两条直线平行;
其中正确的命题个数为( )
| A、0 | ||
| B、1 | ||
| C、π | ||
D、
|
执行如图所示的程序框图,则输出S的值为( )
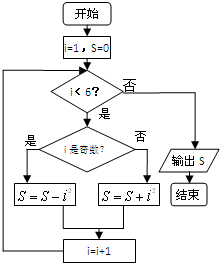

| A、3 | B、-6 | C、10 | D、-15 |
条件p:x≥0,条件q:x2≤x,则p是q的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |