题目内容
已知函数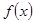 是偶函数,其图像与
是偶函数,其图像与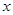 轴有四个不同的交点,则函数
轴有四个不同的交点,则函数 的所
的所
有零点之和为( )
| A.0 | B.8 | C.4 | D.无法确定 |
C
解析试题分析:函数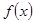 是偶函数,所以图象关于
是偶函数,所以图象关于 轴对称,所以四个零点之和为0,而
轴对称,所以四个零点之和为0,而 是
是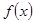 图象向右平移了两个单位,所以零点之和为4.
图象向右平移了两个单位,所以零点之和为4.
考点:本小题主要考查了函数图象的性质和应用以及平移变换,考查学生应用函数图象解题的能力.
点评:偶函数的图象关于 轴对称,奇函数的图象关于原点对称,有时也应用此性质判定函数的奇偶性.
轴对称,奇函数的图象关于原点对称,有时也应用此性质判定函数的奇偶性.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
设偶函数 在
在 上是增函数,则
上是增函数,则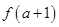 与
与 的
的
大小关系是( )
A. | B. |
C. | D.不能确定 |
若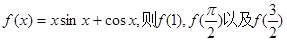 的大小关系是( )
的大小关系是( )
A.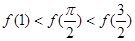 | B. |
C. | D.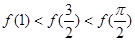 |
函数 的定义域是
的定义域是
A.( ) ) | B.( | C. | D. ) ) |
若函数 的图象过第一二三象限,则有( )
的图象过第一二三象限,则有( )
A. | B. , , |
C. , , | D. |
关于狄利克雷函数 的叙述错误的是 ( )
的叙述错误的是 ( )
A. 的值域是 的值域是 | B. 是偶函数 是偶函数 |
C. 是奇函数 是奇函数 | D. 的定义域是 的定义域是 |
设定义在 上的函数
上的函数 满足
满足 ,若
,若 ,则
,则
A. | B. | C. | D. |
已知函数 ,则函数
,则函数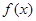 的值域为 ( )
的值域为 ( )
A. | B. | C. | D. |
 ]的函数
]的函数 图像的两个端点为A、B,M(x,y)是
图像的两个端点为A、B,M(x,y)是 图象上任意一点,其中
图象上任意一点,其中 .已知向量
.已知向量 ,若不等式
,若不等式 恒成立, 则称函数
恒成立, 则称函数 在[
在[ 在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
 D.
D.