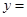题目内容
已知函数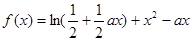 。(
。(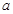 为常数,
为常数,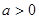 )
)
(Ⅰ)若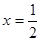 是函数
是函数 的一个极值点,求
的一个极值点,求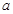 的值;
的值;
(Ⅱ)求证:当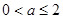 时,
时, 在
在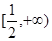 上是增函数;
上是增函数;
(Ⅲ)若对任意的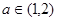 ,总存在
,总存在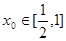 ,使不等式
,使不等式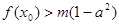 成立,求实数
成立,求实数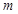 的取值范围。
的取值范围。
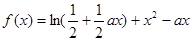 。(
。(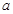 为常数,
为常数,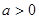 )
)(Ⅰ)若
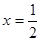 是函数
是函数 的一个极值点,求
的一个极值点,求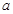 的值;
的值;(Ⅱ)求证:当
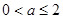 时,
时, 在
在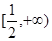 上是增函数;
上是增函数;(Ⅲ)若对任意的
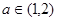 ,总存在
,总存在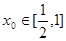 ,使不等式
,使不等式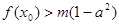 成立,求实数
成立,求实数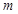 的取值范围。
的取值范围。(Ⅰ)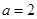 ;(Ⅱ)详见解析;(Ⅲ)实数
;(Ⅱ)详见解析;(Ⅲ)实数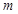 的取值范围为
的取值范围为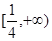
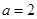 ;(Ⅱ)详见解析;(Ⅲ)实数
;(Ⅱ)详见解析;(Ⅲ)实数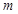 的取值范围为
的取值范围为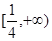
试题分析:(Ⅰ)函数
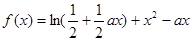 ,
,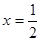 是函数
是函数 的一个极值点,先求出其导函数:
的一个极值点,先求出其导函数: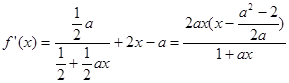 ,利用
,利用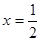 是函数
是函数 的一个极值点对应的结论,即
的一个极值点对应的结论,即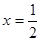 时,它的导函数值为零,可令
时,它的导函数值为零,可令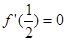 ,即可求
,即可求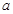 的值;(Ⅱ)求证:当
的值;(Ⅱ)求证:当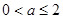 时,
时, 在
在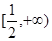 上是增函数,由于
上是增函数,由于 含有对数函数,可通过求导来证明,因此利用:
含有对数函数,可通过求导来证明,因此利用: ,在
,在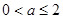 时,分析出因式中的每一项都大于等于0,即得
时,分析出因式中的每一项都大于等于0,即得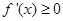 ,从而可证明结论;(Ⅲ)先由(Ⅱ)知,
,从而可证明结论;(Ⅲ)先由(Ⅱ)知, 在
在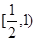 上的最大值为
上的最大值为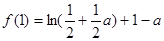 ,把问题转化为对任意的
,把问题转化为对任意的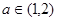 ,不等式
,不等式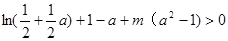 恒成立;然后再利用导函数研究不等式左边的最小值看是否符合要求即可求实数
恒成立;然后再利用导函数研究不等式左边的最小值看是否符合要求即可求实数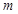 的取值范围为
的取值范围为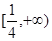 .
.试题解析:
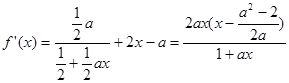
(Ⅰ)由已知,得
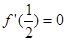 且
且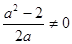 ,
,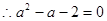

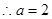 3分
3分(Ⅱ)当
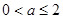 时,
时,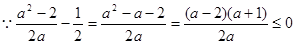
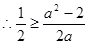
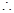 当
当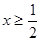 时,
时,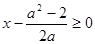 又
又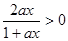
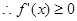
故
 在
在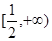 上是增函数 6分
上是增函数 6分(Ⅲ)
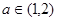 时,由(Ⅱ)知,
时,由(Ⅱ)知, 在
在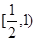 上的最大值为
上的最大值为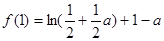
于是问题等价于:对任意的
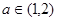 ,不等式
,不等式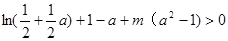 恒成立。
恒成立。记
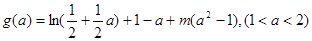
则
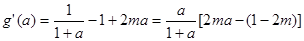
当
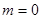 时,
时,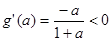
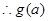 在区间
在区间 上递减,此时
上递减,此时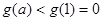
由于
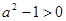 ,
,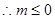 时不可能使
时不可能使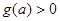 恒成立,故必有
恒成立,故必有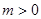
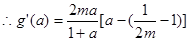
若
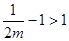 ,可知
,可知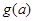 在区间
在区间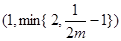 上递减,在此区间上,有
上递减,在此区间上,有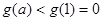 ,与
,与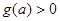 恒成立相矛盾,故
恒成立相矛盾,故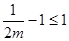 ,这时
,这时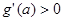 ,
,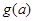 在
在 上递增,恒有
上递增,恒有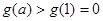 ,满足题设要求,
,满足题设要求,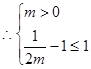 即
即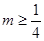
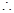 实数
实数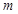 的取值范围为
的取值范围为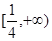 14分
14分
练习册系列答案
相关题目
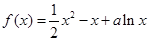 (其中
(其中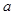 为常数).
为常数).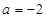 时,求函数
时,求函数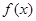 的最值;
的最值;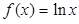 .
.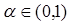 ,求
,求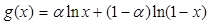 最大值;
最大值;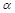 ,
,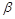 满足
满足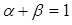 .求证:
.求证: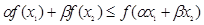 ;
;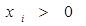 ,正数
,正数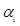 满足
满足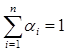 .证明:
.证明: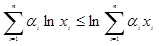
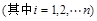 .
.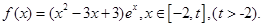
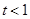 时,求函数
时,求函数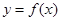 的单调区间;
的单调区间;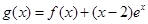 ,试问函数
,试问函数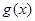 在
在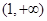 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.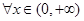 都有
都有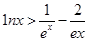 。
。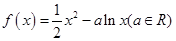 .
.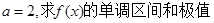 .
.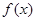 在
在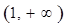 上是增函数,求
上是增函数,求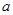 的取值范围.
的取值范围. 满足
满足 ,且
,且 为偶函数,当
为偶函数,当 时,有( )
时,有( )



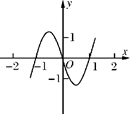
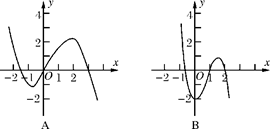
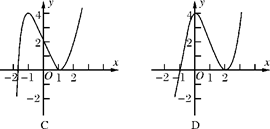
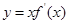 的图象如图所示(其中
的图象如图所示(其中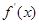 是函数
是函数 的导函数)下面四个图象中,
的导函数)下面四个图象中,