题目内容
经过抛物线y2=2px（p＞0）的焦点F作一直线l交抛物线于A(x1,y1)、B(x2,y2)两点,则
等于（ ）A.4 B.-4 C.p2 D.-p2
解法一：设直线l的方程为my=x- 由 y2-2pmy-p2=0. ∴y1y22=-p2,y1+y2=2pm. ∴x1x2=(my1+ =m2y1y2+ =-p2m+ = ∴ 故选B. 解法二：令l⊥x轴,则x1=x2= ∴x1x2= 答案：B
.
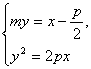消去x,得
)(my2+
)
m(y1+y2)+
m·2pm+
.
=-
=-4.
,y1=p,y2=-p.
,y1y2=-p2.∴
=-4.故选B.
练习册系列答案
小升初衔接教程快乐假期系列答案
书屯文化期末暑假期末冲刺假期作业云南人民出版社系列答案
暑假作业安徽人民出版社系列答案
阳光假日暑假系列答案
优佳学案暑假活动系列答案
赢在课堂激活思维系列答案
金考卷单元专项期中期末系列答案
步步高大一轮复习讲义系列答案
毕业生暑期必读系列答案
相关题目