题目内容
如图所示,直线l:x-y+1=0,点A(1,5),直线AD⊥l于点D,直线AB∥x轴交y轴于点B,l与y轴交于点C.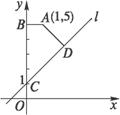
(1)分别求直线AD与AB的方程;
(2)求四边形ABCD的面积.
解析:(1)AD⊥l,kCD=1,∴kAD=-![]() =-1.
=-1.
∴lAD:y-5=-(x-1),即x+y-6=0.
AB∥x轴,即kAB=0,∴方程为y=5.
(2)设C(0,b),由x-y+1=0,得b=1.∴C(0,1).
设D(x0,y0),则y0=x0+1.
由kAD=![]() =-1,得x0=
=-1,得x0=![]() ,y0=
,y0=![]() ,D(
,D(![]() ,
,![]() ).
).
又B(0,5),
∴|BC|=|5-1|=4,|AB|=1,
|CD|=![]()
|AD|=![]() .
.
∴S四边形ABCD=S△ABC+S△ACD
=![]() (|AB|·|BC|+|CD|·|AD|)
(|AB|·|BC|+|CD|·|AD|)
=![]() (1×4+
(1×4+![]() ×
×![]() )
)
=![]() ×
×![]() =
=![]() .
.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
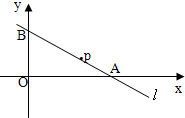 如图所示,直线l过点P(6,2),且和x轴,y轴正方向分别交于A,B两点,求直线l在两坐标轴上截距之和S的最小值及此时直线l的方程.
如图所示,直线l过点P(6,2),且和x轴,y轴正方向分别交于A,B两点,求直线l在两坐标轴上截距之和S的最小值及此时直线l的方程.
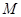 的坐标为
的坐标为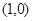 ;
;
