题目内容
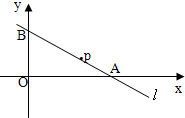 如图所示,直线l过点P(6,2),且和x轴,y轴正方向分别交于A,B两点,求直线l在两坐标轴上截距之和S的最小值及此时直线l的方程.
如图所示,直线l过点P(6,2),且和x轴,y轴正方向分别交于A,B两点,求直线l在两坐标轴上截距之和S的最小值及此时直线l的方程.分析:由题意可设直线l的方程为 y-2=k(x-6)(k<0),令x,y分别为0可得截距,可得S的表达式,由基本不等式可得最值和k值,可得直线的方程.
解答:解:由题意可知直线l的斜率存在且小于零,
故可设直线l的方程为 y-2=k(x-6)(k<0)
令x=0,则y=2-6k,令y=0,则x=6-
∴A(6-
,0),B(0,2-6k),
由k<0,知-k>0,∴6-
>0,2-6k>0,
∴S=2-6k+6-
=8+(-6k)+(-
)≥8+2
=8+4
,
当且仅当-6k=-
,即k=-
时取等号,
∴s的最小值为8+4
,
此时直线l的方程为y-2=-
(x-6),化为一般式可得
x+3y-6-6
=0
故可设直线l的方程为 y-2=k(x-6)(k<0)
令x=0,则y=2-6k,令y=0,则x=6-
| 2 |
| k |
∴A(6-
| 2 |
| k |
由k<0,知-k>0,∴6-
| 2 |
| k |
∴S=2-6k+6-
| 2 |
| k |
| 2 |
| k |
-6k•(-
|
| 3 |
当且仅当-6k=-
| 2 |
| k |
| ||
| 3 |
∴s的最小值为8+4
| 3 |
此时直线l的方程为y-2=-
| ||
| 3 |
| 3 |
| 3 |
点评:本题考查直线的一般式方程,涉及直线的截距和基本不等式求最值,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
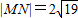 时,求直线l的方程.
时,求直线l的方程.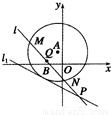
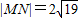 时,求直线l的方程.
时,求直线l的方程.