题目内容
直四棱柱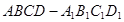 中,底面
中,底面 是等腰梯形,
是等腰梯形,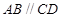 ,
,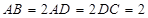 ,
,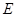 为
为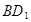 的中点,
的中点, 为
为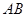 中点.
中点.
(1) 求证: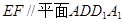 ;
;
(2) 若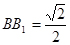 ,求
,求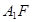 与平面
与平面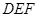 所成角的正弦值.
所成角的正弦值.
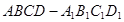 中,底面
中,底面 是等腰梯形,
是等腰梯形,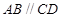 ,
,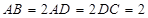 ,
,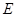 为
为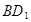 的中点,
的中点, 为
为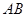 中点.
中点.(1) 求证:
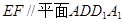 ;
;(2) 若
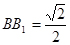 ,求
,求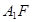 与平面
与平面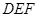 所成角的正弦值.
所成角的正弦值.
解:(1)证明:连结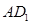 ,在
,在 中
中
∵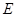 是
是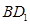 的中点,
的中点, 是
是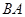 中点,
中点,
∴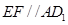
又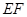
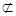 平面
平面 ,
,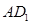 ?平面
?平面
∴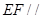 平面
平面 .
.
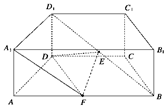
(2)建立如图所示的空间直角坐标系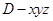 z(
z(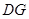 为
为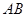 边上的高)
边上的高)
则有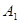 (,-,),
(,-,), (,,0),
(,,0),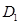 (0 ,0 ,),
(0 ,0 ,),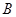 (,,0),
(,,0),
∴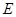 ( ,,),
( ,,),
设平面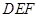 的一个法向量为
的一个法向量为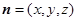 ,
,
由,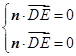 得
得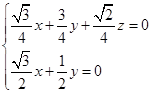
取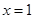 解得
解得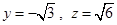 ∴法向量
∴法向量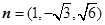
∵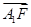 =(0,1,-),
=(0,1,-),
设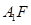 与平面
与平面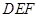 所成的角为
所成的角为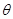 ,则
,则

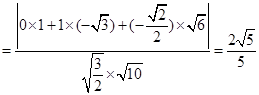
∴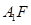 与平面
与平面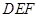 所成角的正弦值为
所成角的正弦值为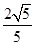 .
.
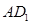 ,在
,在 中
中∵
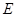 是
是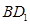 的中点,
的中点, 是
是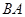 中点,
中点,∴
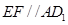
又
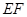
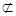 平面
平面 ,
,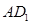 ?平面
?平面
∴
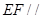 平面
平面 .
.(2)建立如图所示的空间直角坐标系
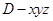 z(
z(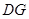 为
为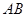 边上的高)
边上的高)则有
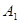 (,-,),
(,-,), (,,0),
(,,0),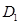 (0 ,0 ,),
(0 ,0 ,),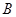 (,,0),
(,,0), ∴
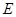 ( ,,),
( ,,),设平面
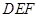 的一个法向量为
的一个法向量为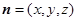 ,
,由,
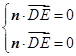 得
得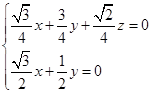
取
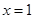 解得
解得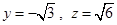 ∴法向量
∴法向量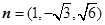
∵
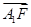 =(0,1,-),
=(0,1,-), 设
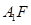 与平面
与平面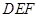 所成的角为
所成的角为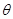 ,则
,则
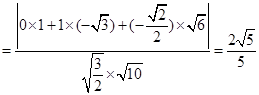
∴
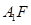 与平面
与平面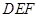 所成角的正弦值为
所成角的正弦值为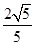 .
.略

练习册系列答案
相关题目

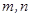 是不同的直线,
是不同的直线,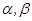 是不重合的平面,给出下面三个命题:
是不重合的平面,给出下面三个命题: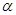 //
//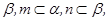 则
则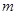 //
//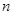 .
.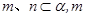 //
//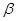 ,
,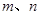 是两条异面直线,若
是两条异面直线,若 、
、 、
、 ,若
,若 中,
中, 是
是 的中点。
的中点。 上求一点
上求一点 ,使
,使 平面
平面 ;
; 的余弦值.
的余弦值.
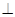 底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点。
底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点。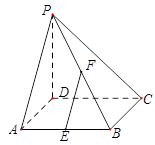




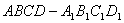 中,以顶点
中,以顶点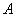 为端点的三条棱长都是
为端点的三条棱长都是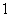 ,且它们彼此的夹角都是
,且它们彼此的夹角都是 ,则以
,则以


