题目内容

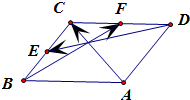
已知平行四边形ABCD，点E、F分别为边BC、CD上的中点，若
AC
=λ
DE
+μ
.
BF
，则λ+μ=
4
4
．
分析：设
AB
=
a
，
AD
=
b
，将则
DE
和
BF
都表示成
a
、
b
的线性组合，再结合已知等式和
AC
=
a
+
b
建立等式，通过比较系数得到关于λ、μ的方程组，解之即得λ+μ的值．
解答：解：设
AB
=
a
，
AD
=
b
，则
DE
=
a
-
1
2
b
，
BF
=
b
-
1
2
a
，
AC
=
a
+
b
，
∵
AC
=λ
DE
+μ
.
BF
，
∴
a
+
b
=λ（
a
-
1
2
b
）+μ（
b
-
1
2
a
），可得
λ-
1
2
μ=1
μ-
1
2
λ=1

解之得，λ=μ=2，故λ+μ=4
故答案为：4
点评：本题在平行四边形中给出一组邻边的中点，将一个向量表示成另外两向量的线性组合，着重考查了平面向量基本定理和向量加减法的定义等知识，属于基础题．
练习册系列答案
相关题目
已知O为△ABC的外心，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
（1）若
OA
=
a
，
OB
=
b
，
OC
=
c
，
OH
=
h
，试用
a
、
b
、
c
表示
h
；
（2）证明：
AH
⊥
BC
；
（3）若△ABC的∠A=60°，∠B=45°，外接圆的半径为R，用R表示|
h
|．
已知以Rt△ABC的直角边AB为直径作⊙O，与斜边AC交于点D，E为BC边上的中点，连结DE.

（1）如图，求证：DE是⊙O的切线；

（2）连结OE、AE，当∠CAB为何值时，四边形AOED是平行四边形，并在此条件下求sin∠CAE的值.

已知O为△ABC的外心，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
（1）若
OA
=
a
，
OB
=
b
，
OC
=
c
，
OH
=
h
，试用
a
、
b
、
c
表示
h
；
（2）证明：
AH
⊥
BC
；
（3）若△ABC的∠A=60°，∠B=45°，外接圆的半径为R，用R表示|
h
|．
已知O为△ABC的外心，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
（1）若，试用表示；
（2）证明：；
（3）若△ABC的∠A=60°，∠B=45°，外接圆的半径为R，用R表示．
已知O为△ABC的外心，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
（1）若，试用表示；
（2）证明：；
（3）若△ABC的∠A=60°，∠B=45°，外接圆的半径为R，用R表示．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网