Question

对于一个有限数列P={P₁，P₂，…，P_n}P的“蔡查罗和”定义为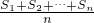，其
中S_k=P₁+P₂+…+P_k（1≤k≤n）．若一个99项的数列{P₁，P₂，…，P₉₉}的“蔡查罗和”为1000，则100项的数列{1，P₁，P₂，…，P₉₉}“蔡查罗和”为

1. A.
   990
2. B.
   991
3. C.
   992
4. D.
   993

Answer 1

B
分析：由“蔡查罗和”定义，{P₁，P₂，，P₉₉}的“蔡查罗和”为，由此可推导出100项的数列{1，P₁，P₂，…，P₉₉}“蔡查罗和”．
解答：由“蔡查罗和”定义，
{P₁，P₂，，P₉₉}的“蔡查罗和”为，
∴S₁+S₂++S₉₉=99000，
则100项的数列{1，P₁，P₂，，P₉₉}“蔡查罗和”为=991．
故选B．
点评：本题考查数列的性质和应用，解题时要认真审题，仔细求解．