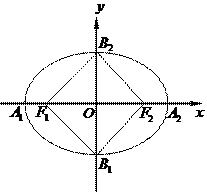题目内容
过抛物线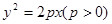 上一定点
上一定点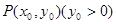 ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于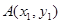 、
、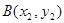 .当
.当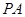 与
与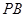 的斜率存在且倾斜角互补时,则
的斜率存在且倾斜角互补时,则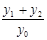 的值为( )
的值为( )
A.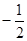 B.
B.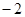 C.
C.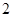 D.无法确定
D.无法确定
【答案】
B
【解析】
试题分析:设直线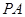 斜率为
斜率为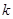 ,则直线
,则直线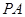 的方程为
的方程为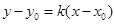 ,与
,与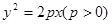 联立方程组消去
联立方程组消去 得:
得: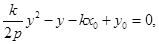 由韦达定理得:
由韦达定理得: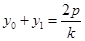 ;因为
;因为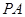 与
与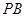 的倾斜角互补,所以
的倾斜角互补,所以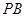 的斜率为
的斜率为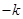 ,同理可得:
,同理可得: ,所以
,所以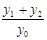
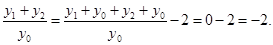
考点:本小题主要考查直线与抛物线的位置关系、韦达定理、倾斜角与斜率的关系等知识,考查了学生分析问题、解答问题的能力和运算求解能力.
点评: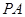 与
与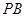 的斜率存在且倾斜角互补,所以它们的斜率互为相反数,从而想到分别设它们的斜率为
的斜率存在且倾斜角互补,所以它们的斜率互为相反数,从而想到分别设它们的斜率为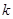 和
和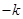 ,从而使问题得到解决.
,从而使问题得到解决.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

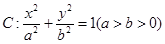 的离心率为
的离心率为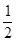 ,
,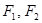 为椭圆的左右焦点,
为椭圆的左右焦点,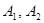 ;
;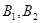 分别为椭圆的长轴和短轴的端点(如图) . 若四边形
分别为椭圆的长轴和短轴的端点(如图) . 若四边形 的面积为
的面积为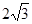 .
.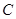 的方程.
的方程.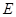
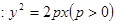 的焦点与椭圆
的焦点与椭圆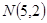 任意作一条直线
任意作一条直线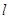 ,交抛物线
,交抛物线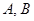 两点. 证明:以
两点. 证明:以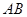 为直径的所有圆是否过抛物线
为直径的所有圆是否过抛物线
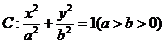 的离心率为
的离心率为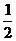 ,
,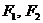 为椭圆的左右焦点,
为椭圆的左右焦点,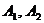 ;
;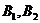 分别为椭圆的长轴和短轴的端点(如图) . 若四边形
分别为椭圆的长轴和短轴的端点(如图) . 若四边形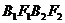 的面积为
的面积为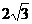 .
.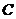 的方程.
的方程.
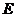
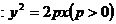 的焦点与椭圆
的焦点与椭圆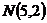 任意作一条直线
任意作一条直线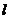 ,交抛物线
,交抛物线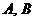 两点. 证明:以
两点. 证明:以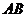 为直径的所有圆是否过抛物线
为直径的所有圆是否过抛物线