题目内容
1.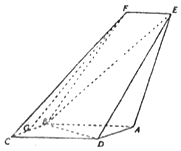 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.(Ⅰ)求证:FG∥平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
(Ⅲ)求直线EF与平面BED所成角的正弦值.
分析 (Ⅰ)取BD的中点为O,连结OE,OG,推导出四边形OGFE是平行四边形,从而FG∥OE,由此能证明FG∥平面BED.
(Ⅱ)由余弦定理得BD=$\sqrt{3}$,由勾股定理得BD⊥AD,从而BD⊥平面AED,由此能证明平面BED⊥平面AED.
(Ⅲ)由EF∥AB,知直线EF与平面BED所成角为直线AB与平面BED所成角,过点A作AH⊥DE于点H,连结BH,直线AB与平面BED所成角即为∠ABH,由此能求出直线EF与平面BED所成角的正弦值.
解答 证明:(Ⅰ)取BD的中点为O,连结OE,OG,
在△BCD中,∵G是BC的中点,
∴OG∥DC,且OG=$\frac{1}{2}DC$=1,
又∵EF∥AB,AB∥DC,∴EF∥OG,且EF=OG,
即四边形OGFE是平行四边形,∴FG∥OE,
又FG?平面BED,OE?平面BED,
∴FG∥平面BED.
(Ⅱ)在△ABD中,AD=1,AB=2,∠BAD=60°,
由余弦定理得BD=$\sqrt{4+1-2×2×1×cos60°}$=$\sqrt{3}$,
∴AD2+BD2=AB2,∴∠ADB=90°,∴BD⊥AD,
又∵平面AED⊥平面ABCD,BD?平面ABCD,平面AED∩平面ABCD=AD,
∴BD⊥平面AED,
又∵平面BD?平面BED,
∴平面BED⊥平面AED.
解:(Ⅲ)∵EF∥AB,∴直线EF与平面BED所成角为直线AB与平面BED所成角,
过点A作AH⊥DE于点H,连结BH,
又∵平面BED∩平面AED=ED,
由(Ⅱ)知AH⊥平面BED,
∴直线AB与平面BED所成角即为∠ABH,
在△ADE中,AD=1,DE=3,AE=$\sqrt{6}$,
由余弦定理得cos∠ADE=$\frac{1+9-6}{2×1×3}$=$\frac{2}{3}$,
∴sin$∠ADE=\sqrt{1-(\frac{2}{3})^{2}}$=$\frac{\sqrt{5}}{3}$,
∴AH=AD$•sin∠ADE=\frac{\sqrt{5}}{3}$,
在Rt△AHB中,sin$∠ABH=\frac{AH}{AB}=\frac{\sqrt{5}}{6}$,
∴直线EF与平面BED所成角的正弦值为$\frac{\sqrt{5}}{6}$.
点评 本题考查线面平行的证明,考查面面垂直的,考查线面角的正弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查等价转化思想、数形结合思想,是中档题.

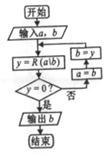 我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )
我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )