题目内容
已知函数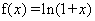 ,
,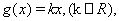
(1)证明:当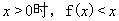 ;
;
(2)证明:当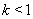 时,存在
时,存在 ,使得对
,使得对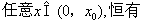
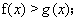
(3)确定k的所以可能取值,使得存在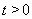 ,对任意的
,对任意的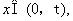 恒有
恒有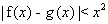 .
.
解法一:(1)令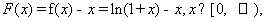 则有
则有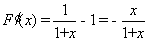
当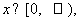
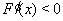 ,所以
,所以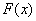 在
在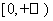 上单调递减,
上单调递减,
故当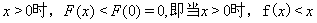 .
.
(2)令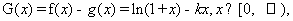 则有
则有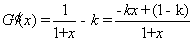
当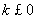
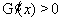 ,所以
,所以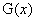 在
在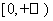 上单调递增,
上单调递增, 
故对任意正实数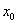 均满足题意.
均满足题意.
当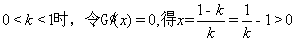 .
.
取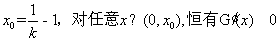 ,所以
,所以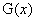 在
在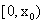 上单调递增,
上单调递增,  ,即
,即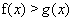 .
.
综上,当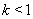 时,总存在
时,总存在 ,使得对任意的
,使得对任意的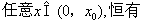
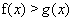 .
.
(3)当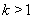 时,由(1)知,对于
时,由(1)知,对于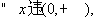
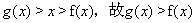 ,
,
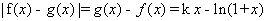 ,
,
令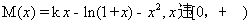 ,则有
,则有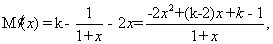
故当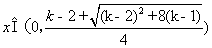 时,
时,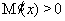 ,
,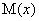 在
在 上单调递增,故
上单调递增,故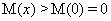 ,即
,即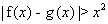 ,所以满足题意的t不存在.
,所以满足题意的t不存在.
当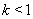 时,由(2)知存在
时,由(2)知存在 ,使得对任意的
,使得对任意的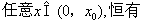
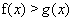 .
.
此时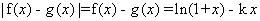 ,
,
令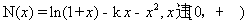 ,则有
,则有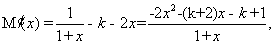
故当 时,
时, ,
,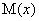 在
在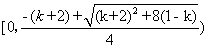 上单调递增,故
上单调递增,故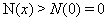 ,即
,即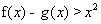 ,记
,记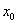 与
与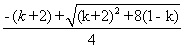 中较小的为
中较小的为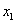 ,
,
则当 ,故满足题意的t不存在.
,故满足题意的t不存在.
当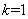 ,由(1)知,
,由(1)知,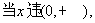
 ,
,
令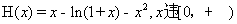 ,则有
,则有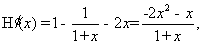
当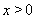 时,
时,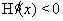 ,所以
,所以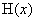 在
在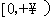 上单调递减,故
上单调递减,故 ,
,
故当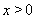 时,恒有
时,恒有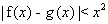 ,此时,任意实数t满足题意.
,此时,任意实数t满足题意.
综上,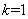 .
.
解法二:(1)(2)同解法一.
(3)当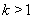 时,由(1)知,对于
时,由(1)知,对于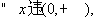
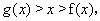 ,
,
故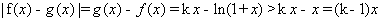 ,
,
令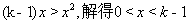 ,
,
从而得到当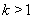 时,
时,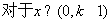 恒有
恒有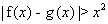 ,所以满足题意的t不存在.
,所以满足题意的t不存在.
当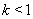 时,取
时,取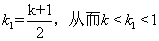
由(2)知存在 ,使得
,使得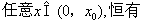
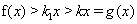 .
.
此时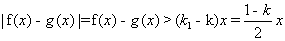 ,
,
令 ,此时
,此时 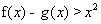 ,
,
记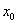 与
与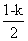 中较小的为
中较小的为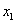 ,则当
,则当 ,
,
故满足题意的t不存在.
当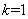 ,由(1)知,
,由(1)知,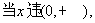
 ,
,
令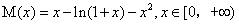 ,则有
,则有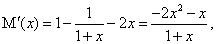
当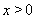 时,
时,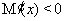 ,所以
,所以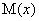 在
在 上单调递减,故
上单调递减,故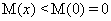 ,
,
故当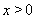 时,恒有
时,恒有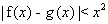 ,此时,任意实数t满足题意.
,此时,任意实数t满足题意.
综上,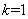 .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
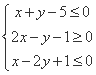 ,则z=2x+y的最大值为 .
,则z=2x+y的最大值为 . 是函数
是函数 的两个不同的零点,且
的两个不同的零点,且 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则
这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 的值等于
的值等于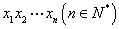 ,其中
,其中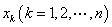 称为第
称为第 位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)
位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)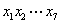 的码元满足如下校验方程组:
的码元满足如下校验方程组: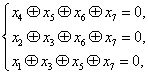
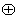 定义为:
定义为: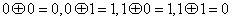 .
. ”是“
”是“ ”的
”的 ,
, ,则
,则
 B.
B. C.
C. D.
D.