题目内容
已知数列{an}的通项公式为an=
(n∈N*),其前n项和
=
,则双曲线
-
=1的渐近线方程为( )
| 1 |
| n(n+1) |
| S | n |
| 9 |
| 10 |
| x2 |
| n+1 |
| y2 |
| n |
A.y=±
| B.y=±
| C.y=±
| D.y=±
|
∵数列{an}的通项公式为an=
(n∈N*),
∴an=
-
,可得
=(1-
)+(
-
)+…+(
-
)+(
-
)=
即1-
=
,解之得n=9.
∴双曲线的方程为
-
=1,得a=
,b=3
因此该双曲线的渐近方程为y=±
x,即y=±
x.
故选:C
| 1 |
| n(n+1) |
∴an=
| 1 |
| n |
| 1 |
| n+1 |
| S | n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
| 9 |
| 10 |
即1-
| 1 |
| n+1 |
| 9 |
| 10 |
∴双曲线的方程为
| x2 |
| 10 |
| y2 |
| 9 |
| 10 |
因此该双曲线的渐近方程为y=±
| b |
| a |
3
| ||
| 10 |
故选:C

练习册系列答案
相关题目
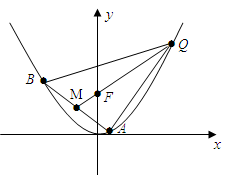
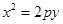 的焦点为F,
的焦点为F,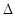 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,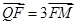 .(1)若M
.(1)若M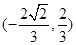 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若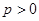 的常数,试求线段
的常数,试求线段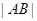 长的最大值.
长的最大值.