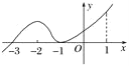
题目内容
【题目】已知函数![]() .
.
(1)若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值
的最大值![]() ;
;
(2)在(1)成立的条件下,正实数![]() ,
,![]() 满足
满足![]() ,证明:
,证明:![]() .
.
【答案】(1)2;(2)证明见解析.
【解析】
(1)由题意可得![]() ,则原问题等价于
,则原问题等价于![]() ,据此可得实数
,据此可得实数![]() 的最大值
的最大值![]() .
.
(2)证明:法一:由题意结合(1)的结论可知![]() ,结合均值不等式的结论有
,结合均值不等式的结论有![]() ,据此由综合法即可证得
,据此由综合法即可证得![]() .
.
法二:利用分析法,原问题等价于![]() ,进一步,只需证明
,进一步,只需证明![]() ,分解因式后只需证
,分解因式后只需证![]() ,据此即可证得题中的结论.
,据此即可证得题中的结论.
(1)由已知可得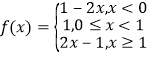 ,
,
所以![]() ,
,
所以只需![]() ,解得
,解得![]() ,
,
∴![]() ,所以实数
,所以实数![]() 的最大值
的最大值![]() .
.
(2)证明:法一:综合法
∵![]() ,
,
∴![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() 时取等号,①
时取等号,①
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() 时取等号,②
时取等号,②
由①②得,∴![]() ,所以
,所以![]() .
.
法二:分析法
因为![]() ,
,![]() ,
,
所以要证![]() ,只需证
,只需证![]() ,
,
即证![]() ,
,
∵![]() ,所以只要证
,所以只要证![]() ,
,
即证![]() ,
,
即证![]() ,因为
,因为![]() ,所以只需证
,所以只需证![]() ,
,
因为![]() ,所以
,所以![]() 成立,
成立,
所以![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目