题目内容
18.设x,y是正实数,记S为x,$y+\frac{1}{x}$,$\frac{1}{y}$中的最小值,则S的最大值为$\sqrt{2}$.分析 设a=x,b=$\frac{1}{y}$,c=y+$\frac{1}{x}$=$\frac{1}{a}$+$\frac{1}{b}$都大于0.不妨设a≤b.可得$\frac{1}{b}$+$\frac{1}{b}$-b≤c-a=$\frac{1}{a}$+$\frac{1}{b}$-a≤$\frac{1}{a}$+$\frac{1}{a}$-a.即$\frac{2-{b}^{2}}{b}$≤c-a≤$\frac{2-{a}^{2}}{a}$.对a与$\sqrt{2}$的大小分类讨论即可得出最大值.
解答 解:设a=x,b=$\frac{1}{y}$,c=y+$\frac{1}{x}$=$\frac{1}{b}$+$\frac{1}{a}$.都大于0.
不妨设a≤b.则$\frac{1}{a}$≥$\frac{1}{b}$.
则$\frac{1}{b}$+$\frac{1}{b}$-b≤c-a=$\frac{1}{a}$+$\frac{1}{b}$-a≤$\frac{1}{a}$+$\frac{1}{a}$-a.
∴$\frac{2-{b}^{2}}{b}$≤c-a≤$\frac{2-{a}^{2}}{a}$,
①当a≥$\sqrt{2}$时,c≤a,此时c最小;
②当0<a<$\sqrt{2}$,c-a≥0,此时a最小,S≤$\sqrt{2}$.
综上可得:S的最大值为:$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了不等式的性质、分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
9.如图,在矩形 OABC中,$\overrightarrow{{A}{B}}=3\overrightarrow{{A}{E}}$,$\overrightarrow{{B}C}=3\overrightarrow{FC}$,若$\overrightarrow{{O}{B}}=λ\overrightarrow{{O}{E}}+μ\overrightarrow{{O}F}$(λ,μ∈R),则λμ等于( )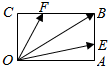

| A. | $\frac{9}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{4}{9}$ | D. | $\frac{16}{9}$ |
7.已知f(x)=log2x,则f-1(x)满足( )
| A. | f-1(2x)=2f-1(x) | B. | f-1(2x)=$\frac{1}{2}$f-1(x) | C. | f-1(2x)=[f-1(x)]2 | D. | f-1(2x)=[f-1(x)]${\;}^{\frac{1}{2}}$ |
8.用max{a,b,c}表示a,b,c三个数中的最大值,设f(x)=max{2x,x+2,10-x}(x≥0),则f(x)取得最小值时x所在区间为( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |