题目内容
已知直线l1:4x-3y+6=0和直线l2:x=-
,若抛物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2,则抛物线C的方程为 .
| p |
| 2 |
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:设出抛物线上一点P的坐标,然后利用点到直线的距离公式分别求出P到直线l1和直线l2的距离d1和d2,求出d1+d2,利用二次函数求最值的方法,求出距离之和的最小值,即可得出结论.
解答:
解:设抛物线上的一点P的坐标为(
a2,2a),则P到直线l2:x=-
的距离d2=
a2+
;
P到直线l1:4x-3y+6=0的距离d1=
,
则d1+d2=
+
a2+
=
a2-
a+
+
,
当a=
时,P到直线l1和直线l2的距离之和的最小值为2,
∴p=2,
∴抛物线C的方程为y2=4x
故答案为:y2=4x.
| 2 |
| p |
| p |
| 2 |
| 2 |
| p |
| p |
| 2 |
P到直线l1:4x-3y+6=0的距离d1=
|
| ||
| 5 |
则d1+d2=
|
| ||
| 5 |
| 2 |
| p |
| p |
| 2 |
| 18 |
| 5p |
| 6 |
| 5 |
| 6 |
| 5 |
| p |
| 2 |
当a=
| p |
| 3 |
∴p=2,
∴抛物线C的方程为y2=4x
故答案为:y2=4x.
点评:此题考查学生灵活运用抛物线的简单性质解决实际问题,灵活运用点到直线的距离公式化简求值,是一道中档题.

练习册系列答案
相关题目
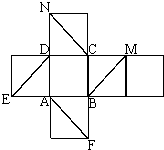 如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是
如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是