题目内容
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
,
(I)求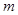 与
与 的关系式;
的关系式;
(II)求 的单调区间;
的单调区间;
(III)当 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3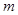 ,求
,求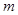 的取值范围.
的取值范围.
【答案】
(1) ;(2)见解析;(3)
;(2)见解析;(3) .
.
【解析】本小题主要考查利用导数求函数的单调区间,恒成立问题,考查分类讨论的思想方法.
解: (I) 因为
因为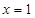 是函数
是函数 的一个极值点,
的一个极值点,
所以 ,即
,即 ,所以
,所以 ………………4分
………………4分
(II)由(I)知, =
= …………5分
…………5分
当 时,有
时,有 ,当
,当 变化时,
变化时, 与
与 的变化如下表:
的变化如下表:
|
|
|
|
|
1 |
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
|
|
|
|
|
|
单调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
……………………………………7分
故有上表知,当 时,
时, 在
在 单调递减,
单调递减,
在 单调递增,在
单调递增,在 上单调递减. ………………………………9分
上单调递减. ………………………………9分
(III)由已知得 ,即
,即
又 所以
所以 即
即 ①
①
设 ,其函数开口向上,由题意知①式恒成立,……10分
,其函数开口向上,由题意知①式恒成立,……10分
所以 解之得………………12分
解之得………………12分
所以 ……………………………13分
……………………………13分
即 的取值范围为
的取值范围为 …………………………14分
…………………………14分

练习册系列答案
相关题目



 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 与
与 的关系式;
的关系式; 的单调区间;
的单调区间;
 ;试比较g(x)与
;试比较g(x)与 的大小。
的大小。 是函数
是函数 的一个极值点.
的一个极值点.
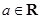

 的值;
的值; ,
, 时,证明:
时,证明:
 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与 的关系式;
的关系式;  的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求
,求 的取值范围.
的取值范围. 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 。
。 与
与 的关系表达式;
的关系表达式; 的单调区间;
的单调区间; 时,函数
时,函数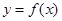 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求实数
,求实数 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与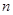 的关系式;
的关系式; 的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3