题目内容
已知直线l1:ax-2y=2a-4,l2:2x+a2y=2a2+4,当0<a<2时,直线l1,l2与两坐标轴围成一个四边形,当四边形的面积最小时,则a=________.
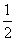 解析:由题意知直线l1,l2恒过定点P(2,2),直线l1的纵截距为2-a,直线l2的横截距为a2+2,所以四边形的面积S=
解析:由题意知直线l1,l2恒过定点P(2,2),直线l1的纵截距为2-a,直线l2的横截距为a2+2,所以四边形的面积S=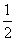 ×2×(2-a)+
×2×(2-a)+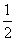 ×2×(a2+2)=a2-a+4=
×2×(a2+2)=a2-a+4= +
+ ,当a=
,当a=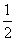 时,面积最小.
时,面积最小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的单调区间;
的单调区间; 在
在 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值; 成立,求实数a的取值范围.
成立,求实数a的取值范围.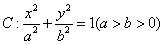 的短半轴长为
的短半轴长为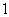 ,动点
,动点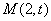
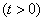 在直线
在直线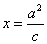 (
(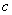 为半焦距)上.
为半焦距)上. 为直径且被直线
为直径且被直线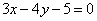 截得的弦长为
截得的弦长为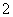 的圆的方程;
的圆的方程;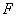 是椭圆的右焦点,过点
是椭圆的右焦点,过点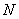 ,
,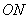 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.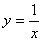 的图像
的图像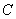 是以
是以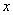 轴与
轴与 轴为渐近线的等轴双曲线.
轴为渐近线的等轴双曲线.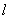 过点
过点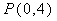 ,且与双曲线
,且与双曲线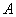 、
、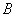 两点,与
两点,与 .
.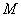 的轨迹方程;
的轨迹方程;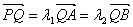 ,且
,且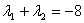 时,求点
时,求点