题目内容
7．在数列{an}中，a1=2，2an+1=2an+1，则a101的值为（ ）| A． | 49 | B． | 50 | C． | 51 | D． | 52 |
分析 先利用递推关系得出其为等差数列，再代入等差数列的通项公式即可．
解答 解：由2an+1=2an+1，得an+1-an=$\frac{1}{2}$，
故为首项为2，公差为$\frac{1}{2}$的等差数列，所以a101=a1+100d=2+100×$\frac{1}{2}$=52．
故选：D．
点评 本题是对数列递推关系式的考查．做这一类型题时，要注意观察递推关系式，找到其隐含的结论，来解题．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
19．与-$\frac{π}{2}$终边相同的角是（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |
1．
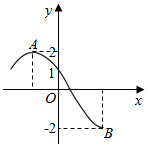如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤$\frac{π}{2}$）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）
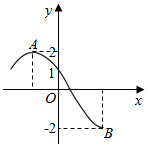如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤$\frac{π}{2}$）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）| A． | -1 | B． | -$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 1 |