题目内容
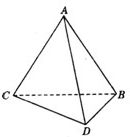
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
(1)求证:平面ABD⊥平面ACD;
(2)求二面角A-CD-B的平面角的正切值;
(3)求异面直线AD与BC间的距离.
(1)求证:平面ABD⊥平面ACD;
(2)求二面角A-CD-B的平面角的正切值;
(3)求异面直线AD与BC间的距离.

证明:(1)∵平面BCD⊥平面ABC,BD⊥BC,平面BCD∩平面ABC=BC
∴BD⊥平面ABC,AC?平面ABC,
∴AC⊥BD,又AC⊥AB,BD∩AB=B,
∴AC⊥平面ABD又AC?平面ACD,
∴平面ABD⊥平面ACD.
(2)设BC中点为E,连AE,过E作EF⊥CD于F,连AF,由三垂线定理:∠EFA为二面角的平面角
∵△EFC∽△DBC,∴
=
,
∴EF=
,又AE=3,
∴tan∠EFA=
=2
∴二面角的平面角的正切值为2
(3)过点D作DG∥BC,且CB=DG,连AG,设平面ADG为平面α
∵BC∥平面ADG,∴B到平面ADG的距离等于C到平面ADG的距离为h
∵VC-AGD=VA-CBD
∴
S△AGDh=
S△BCDAE
∴h=
∴BD⊥平面ABC,AC?平面ABC,
∴AC⊥BD,又AC⊥AB,BD∩AB=B,
∴AC⊥平面ABD又AC?平面ACD,
∴平面ABD⊥平面ACD.
(2)设BC中点为E,连AE,过E作EF⊥CD于F,连AF,由三垂线定理:∠EFA为二面角的平面角
∵△EFC∽△DBC,∴
| EF |
| BD |
| CF |
| CD |
∴EF=
| 3 |
| 2 |
∴tan∠EFA=
| AE |
| EF |
∴二面角的平面角的正切值为2
(3)过点D作DG∥BC,且CB=DG,连AG,设平面ADG为平面α
∵BC∥平面ADG,∴B到平面ADG的距离等于C到平面ADG的距离为h
∵VC-AGD=VA-CBD
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴h=
6
| ||
| 7 |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目