题目内容
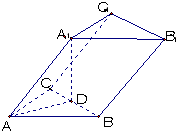
如图:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD为矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中点,
(1)求二面角α-l-β的大小
(2)求证:MN⊥AB
(3)求异面直线PA和MN所成角的大小.

(1)求二面角α-l-β的大小
(2)求证:MN⊥AB
(3)求异面直线PA和MN所成角的大小.

(1)连接PD,∵PA⊥α.∠ADC=90°.
∴∠PDC=90°(三垂线定理).
∠ADP为二面角α-l-β的平面角.
∴△PAD为等腰直角三角形.
∴二面角α-l-β为45°.
(2)设E为DC中点, 连接NE,
连接NE,
则NE∥PD,ME∥AD.
由面面平行的判定定理得:
平面MEN∥平面APD.
AB∥CD
∵CD⊥平面APD
∴AB⊥平面APD
∴AB⊥平面MEN.
∴AB⊥MN.
(3)设F为DP中点.连接AG,GN
则FN=
DC=AM.FN∥DC∥AM.
∴FNMA为平行四边形
则异面直线PA与MN的夹角为∠FAP
∠FAP=
∠PAD=45°(等腰直角三角形DAP上直角的一半).
∴∠PDC=90°(三垂线定理).
∠ADP为二面角α-l-β的平面角.
∴△PAD为等腰直角三角形.
∴二面角α-l-β为45°.
(2)设E为DC中点,
 连接NE,
连接NE,则NE∥PD,ME∥AD.
由面面平行的判定定理得:
平面MEN∥平面APD.
AB∥CD
∵CD⊥平面APD
∴AB⊥平面APD
∴AB⊥平面MEN.
∴AB⊥MN.
(3)设F为DP中点.连接AG,GN
则FN=
| 1 |
| 2 |
∴FNMA为平行四边形
则异面直线PA与MN的夹角为∠FAP
∠FAP=
| 1 |
| 2 |

练习册系列答案
相关题目