Question

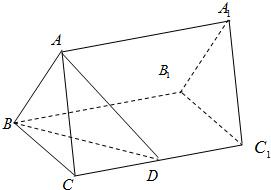如图，已知正三棱柱ABC-A₁B₁C₁的底边长是2，侧棱CC₁的长是2

2

，点D是侧棱CC₁的中点，求直线AD与侧面BB₁C₁C所成的角．

Answer 1

分析：取BC中点E，连接AE，连接ED，根据线面所成角的定义可知∠ADE为直线AD与侧面BB₁C₁C所成角，在Rt△AED中求出此角即可．

解答：解：取BC中点E，连接AE，
∵△ABC是正三角形，
∴AE⊥BC
又底面ABC⊥侧面BB₁C₁C，且两平面交线为BC
∴AE⊥侧面BB₁C₁C
连接ED，则∠ADE为直线AD与侧面BB₁C₁C所成角
在正三角形ABC中，∵BC=2，∴AE=

3

在直角三角形ECD中，∵EC=1，CD=

2

∴ED=

3

在Rt△AED中，∵AE=ED，∴∠ADE=45°
∴直线AD与侧面BB₁C₁C所成的角为45°

点评：本题主要考查了空间中直线与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于中档题．