题目内容
无论m为任何实数,直线l:y=x+m与双曲线C: (b>0)恒有公共点
(b>0)恒有公共点(1)求双曲线C的离心率e的取值范围.
(2)若直线l过双曲线C的右焦点F,与双曲线交于P,Q两点,并且满足
 ,求双曲线C的方程.
,求双曲线C的方程.
【答案】分析:(1)欲求双曲线C的离心率e的取值范围,只需找到a,c 的齐次不等式,根据直线l:y=x+m与双曲线C: (b>0)恒有公共点,联立方程后,方程组必有解,△≥0成立,即可得到含a,c的齐次不等式,离心率e的取值范围可得.
(b>0)恒有公共点,联立方程后,方程组必有解,△≥0成立,即可得到含a,c的齐次不等式,离心率e的取值范围可得.
(2)先设直线l的方程,与双曲线方程联立,求出y1,y2,代入 ,化简,即可求出b2,代入
,化简,即可求出b2,代入 即可.
即可.
解答:解:(1)联立 ,得b2x2-2(x+m)2-2b2=0
,得b2x2-2(x+m)2-2b2=0
(b2-2)x2-4mx-2(m2+b2)=0
当b2=2时,m=0,直线与双曲线无交点,矛盾
∴b2≠2.∴e≠ .
.
∵直线与双曲线恒有交点,△=16m2+8(b2-2)(m2+b2)≥0恒成立
∴16m2+8(b2-2)m2+8(b2-2)b2≥0
∴b2≥2-m2,∴e≥ .e>
.e> .
.
(2)F(c,0).L,y=x-c,
 ,(b2-2)y2+2cb2y+b2c2-2b2=0
,(b2-2)y2+2cb2y+b2c2-2b2=0
∴
∵ ,∴
,∴ ,
,
整理得, =
=
∵b2>0,∴c2-2=b2, =
= ,∴b2=7
,∴b2=7
∴双曲线C的方程为
点评:本题考查了双曲线离心率范围的求法,以及直线与双曲线位置关系的判断,属于综合题.
 (b>0)恒有公共点,联立方程后,方程组必有解,△≥0成立,即可得到含a,c的齐次不等式,离心率e的取值范围可得.
(b>0)恒有公共点,联立方程后,方程组必有解,△≥0成立,即可得到含a,c的齐次不等式,离心率e的取值范围可得.(2)先设直线l的方程,与双曲线方程联立,求出y1,y2,代入
 ,化简,即可求出b2,代入
,化简,即可求出b2,代入 即可.
即可.解答:解:(1)联立
 ,得b2x2-2(x+m)2-2b2=0
,得b2x2-2(x+m)2-2b2=0(b2-2)x2-4mx-2(m2+b2)=0
当b2=2时,m=0,直线与双曲线无交点,矛盾
∴b2≠2.∴e≠
 .
.∵直线与双曲线恒有交点,△=16m2+8(b2-2)(m2+b2)≥0恒成立
∴16m2+8(b2-2)m2+8(b2-2)b2≥0
∴b2≥2-m2,∴e≥
 .e>
.e> .
.(2)F(c,0).L,y=x-c,
 ,(b2-2)y2+2cb2y+b2c2-2b2=0
,(b2-2)y2+2cb2y+b2c2-2b2=0 ∴

∵
 ,∴
,∴ ,
,整理得,
 =
=
∵b2>0,∴c2-2=b2,
 =
= ,∴b2=7
,∴b2=7∴双曲线C的方程为

点评:本题考查了双曲线离心率范围的求法,以及直线与双曲线位置关系的判断,属于综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
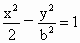 (b>0)恒有公共点.
(b>0)恒有公共点.
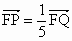 ,求双曲线C的方程.
,求双曲线C的方程.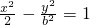 (b>0)恒有公共点
(b>0)恒有公共点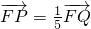 ,求双曲线C的方程.
,求双曲线C的方程.