题目内容
12.设实数x,y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}\right.$,则u=$\frac{1}{x}$+$\frac{1}{2y}$的取值范围是[$\frac{1}{2}$,$\frac{4}{5}$].分析 画出约束条件表示的可行域,显然当x,y都取得最大值时u取得最小值,当u取得最大值时,点(x,y)必在可行域的边界上,此时根据基本不等式求出u的最大值.
解答 解:作出约束条件表示的可行域如图: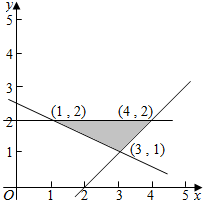
由可行域可知当x=4,y=2时,u=$\frac{1}{x}+\frac{1}{2y}$取得最小值$\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$.
当点(x,y)落在直线x+2y-5=0上某处时,u=$\frac{1}{x}+\frac{1}{2y}$取得最小值.
此时,x+2y=5,2xy≤($\frac{x+2y}{2}$)2=$\frac{25}{4}$.
∴u=$\frac{1}{x}+\frac{1}{2y}=\frac{x+2y}{2xy}=\frac{5}{2xy}$≥$\frac{4}{5}$.
当且仅当x=2y,即x=$\frac{5}{2}$,y=$\frac{5}{4}$时取等号.显然点($\frac{5}{2},\frac{5}{4}$)在可行域内.
故答案为:[$\frac{1}{2}$,$\frac{4}{5}$].
点评 平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
4.函数f(x)=2x+1在区间[1,2]上的平均变化率是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 1 | D. | 3$ |
 如图,在三棱锥P-ABC中,E、F分别为AC、BC的中点.
如图,在三棱锥P-ABC中,E、F分别为AC、BC的中点.