题目内容
已知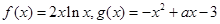 。
。
(1)求函数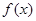 的最小值;
的最小值;
(2)若存在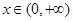 ,使
,使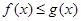 成立,求实数
成立,求实数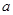 的取值范围。
的取值范围。
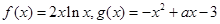 。
。(1)求函数
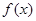 的最小值;
的最小值;(2)若存在
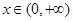 ,使
,使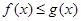 成立,求实数
成立,求实数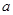 的取值范围。
的取值范围。(1)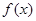 取最小值为
取最小值为 。 (2)
。 (2) 。
。
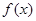 取最小值为
取最小值为 。 (2)
。 (2) 。
。 本试题主要是考查了函数的最值和不等式的恒成立的问题的综合运用。
(1)利用函数的定义域,求解函数的导数,然后令导数大于零或者导数小于零得到结论。
(2)存在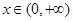 ,使
,使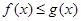 成立,即
成立,即 在
在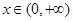 能成立,等价于
能成立,等价于 在
在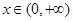 能成立,运用等价转化思想得到
能成立,运用等价转化思想得到 ,然后求解右边函数的最小值即可
,然后求解右边函数的最小值即可
解:(1)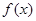 的定义域为
的定义域为 ,
, , ………2分
, ………2分
令 ,得
,得 ,
,
当 时,
时, ;当
;当 时,
时, , ………4分
, ………4分
所以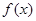 在
在 上单调递减;在
上单调递减;在 上单调递增,
上单调递增,
故当 时
时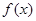 取最小值为
取最小值为 。 ……6分
。 ……6分
(2)存在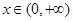 ,使
,使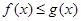 成立,即
成立,即 在
在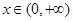 能成立,等价于
能成立,等价于 在
在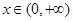 能成立;
能成立;
等价于 ………9分
………9分
记 ,
,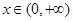
则
当 时,
时, ;当
;当 时,
时, ,
,
所以当 时
时 取最小值为4,故
取最小值为4,故 。
。
(1)利用函数的定义域,求解函数的导数,然后令导数大于零或者导数小于零得到结论。
(2)存在
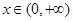 ,使
,使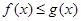 成立,即
成立,即 在
在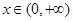 能成立,等价于
能成立,等价于 在
在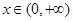 能成立,运用等价转化思想得到
能成立,运用等价转化思想得到 ,然后求解右边函数的最小值即可
,然后求解右边函数的最小值即可解:(1)
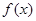 的定义域为
的定义域为 ,
, , ………2分
, ………2分令
 ,得
,得 ,
,当
 时,
时, ;当
;当 时,
时, , ………4分
, ………4分所以
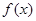 在
在 上单调递减;在
上单调递减;在 上单调递增,
上单调递增,故当
 时
时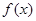 取最小值为
取最小值为 。 ……6分
。 ……6分(2)存在
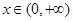 ,使
,使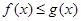 成立,即
成立,即 在
在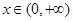 能成立,等价于
能成立,等价于 在
在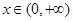 能成立;
能成立;等价于
 ………9分
………9分记
 ,
,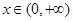
则

当
 时,
时, ;当
;当 时,
时, ,
,所以当
 时
时 取最小值为4,故
取最小值为4,故 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
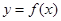 对任意的实数
对任意的实数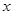 ,都有
,都有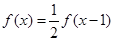 ,且当
,且当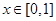 时,
时,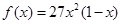 。
。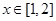 时,求
时,求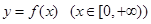 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点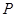 ,使得函数在点
,使得函数在点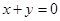 平行。若存在,那么这样的点
平行。若存在,那么这样的点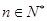 ,且
,且 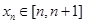 ,记
,记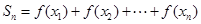 ,求证:
,求证: 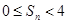 。
。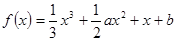
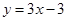 , 求
, 求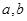 的值;
的值;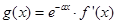 , 求函数
, 求函数 的单调区间.
的单调区间. 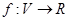 满足:对任意向量
满足:对任意向量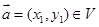
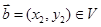 ,以及任意
,以及任意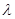 ∈R,均有
∈R,均有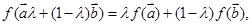 则称映射
则称映射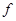 具有性质P.现给出如下映射:
具有性质P.现给出如下映射: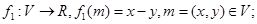
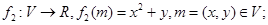
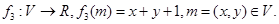
 与
与
 分别相交于点
分别相交于点 ,且曲线
,且曲线 和
和 在点
在点 的值;
的值; 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数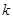 的值
的值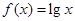 ,若
,若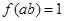 ,则
,则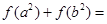
 为定义在R上的偶函数,在
为定义在R上的偶函数,在 时
时 恒成立,且
恒成立,且 ,则不等式
,则不等式 的解集为 .
的解集为 . 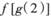 的值为
的值为
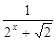 ,利用课本中推导等差数列前n项和的公式的方法,
,利用课本中推导等差数列前n项和的公式的方法,