题目内容
已知函数 与
与
(1)设直线 分别相交于点
分别相交于点 ,且曲线
,且曲线 和
和 在点
在点 处的切线平行,求实数
处的切线平行,求实数 的值;
的值;
(2) 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(3)在(2)的条件下且当 取
取 最大值的
最大值的 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数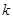 的值
的值
 与
与
(1)设直线
 分别相交于点
分别相交于点 ,且曲线
,且曲线 和
和 在点
在点 处的切线平行,求实数
处的切线平行,求实数 的值;
的值;(2)
 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;(3)在(2)的条件下且当
 取
取 最大值的
最大值的 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数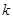 的值
的值(1)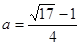 (2)
(2) 的最大值为
的最大值为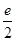 (3)
(3)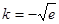
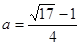 (2)
(2) 的最大值为
的最大值为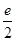 (3)
(3)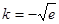
(1)先对f(x)和g(x)求导,由题意可知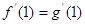 ,从而建立关于a的方程,解出a的值.
,从而建立关于a的方程,解出a的值.
(2)本小题的关键是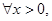
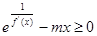 恒成立,转化为
恒成立,转化为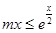 ,即
,即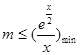 ,
,
然后构造函数 ,利用导数求其最小值即可.
,利用导数求其最小值即可.
(3) 解本小题的关键是在(2)的基础上可知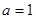 ,
,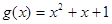 在
在 上的最小值
上的最小值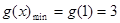 ,从而确定出
,从而确定出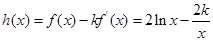 在
在 的最小值为3.下面再利用导数研究h(x)的最小值,根据最小值为3建立关于k的方程求出k的值
的最小值为3.下面再利用导数研究h(x)的最小值,根据最小值为3建立关于k的方程求出k的值
(1)由已知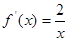 ,
,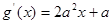 ,曲线
,曲线 和
和 在点
在点 处的切线平行,故
处的切线平行,故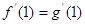 可得:
可得: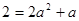 且
且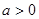 解得:
解得: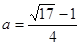 ---3分
---3分
(2)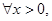
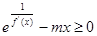 恒成立,即
恒成立,即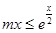 ,即
,即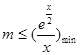 ,---4分
,---4分
记 ,
,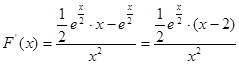 ,---5分
,---5分
当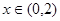 时,
时,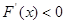 ,
,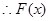 在
在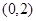 上单调递减
上单调递减
当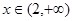 时,
时,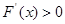 ,
,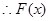 在
在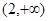 上单调递增 ---7分
上单调递增 ---7分
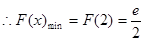 ,故
,故 的最大值为
的最大值为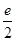 ---8分
---8分
(3)由(2)可知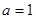 ,故
,故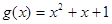 在
在 时,
时,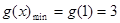
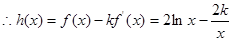 在
在 的最小值为3,
的最小值为3,
令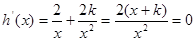 ,解得:
,解得: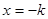 ---10分
---10分
(Ⅰ)当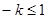 即
即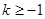 时,
时,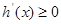 ,此时
,此时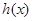 在
在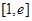 上单调递增
上单调递增
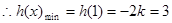 ,解得:
,解得: (不合前提) ---11分
(不合前提) ---11分
(Ⅱ)当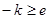 即
即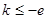 时,
时,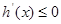 ,此时
,此时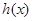 在
在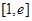 上单调递减
上单调递减
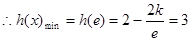 ,解得:
,解得: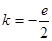 (不合前提)---12分
(不合前提)---12分
(Ⅲ)当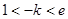 即
即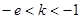 时,
时,
当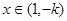 时,
时,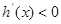 ,
,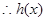 在
在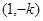 单调递减
单调递减
当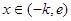 时,
时,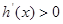 ,
,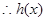 在
在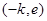 单调递增
单调递增
此时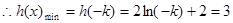 ,解得:
,解得: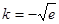 满足前提
满足前提
综上可得: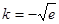
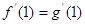 ,从而建立关于a的方程,解出a的值.
,从而建立关于a的方程,解出a的值.(2)本小题的关键是
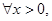
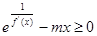 恒成立,转化为
恒成立,转化为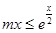 ,即
,即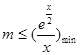 ,
,然后构造函数
 ,利用导数求其最小值即可.
,利用导数求其最小值即可.(3) 解本小题的关键是在(2)的基础上可知
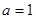 ,
,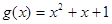 在
在 上的最小值
上的最小值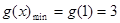 ,从而确定出
,从而确定出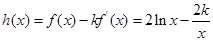 在
在 的最小值为3.下面再利用导数研究h(x)的最小值,根据最小值为3建立关于k的方程求出k的值
的最小值为3.下面再利用导数研究h(x)的最小值,根据最小值为3建立关于k的方程求出k的值(1)由已知
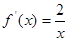 ,
,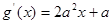 ,曲线
,曲线 和
和 在点
在点 处的切线平行,故
处的切线平行,故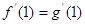 可得:
可得: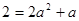 且
且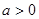 解得:
解得: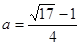 ---3分
---3分(2)
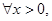
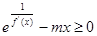 恒成立,即
恒成立,即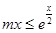 ,即
,即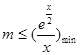 ,---4分
,---4分记
 ,
,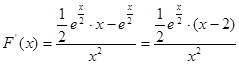 ,---5分
,---5分当
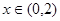 时,
时,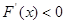 ,
,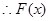 在
在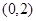 上单调递减
上单调递减当
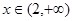 时,
时,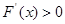 ,
,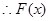 在
在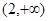 上单调递增 ---7分
上单调递增 ---7分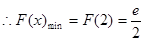 ,故
,故 的最大值为
的最大值为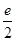 ---8分
---8分(3)由(2)可知
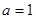 ,故
,故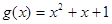 在
在 时,
时,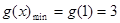
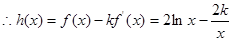 在
在 的最小值为3,
的最小值为3,令
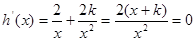 ,解得:
,解得: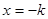 ---10分
---10分(Ⅰ)当
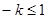 即
即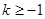 时,
时,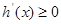 ,此时
,此时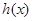 在
在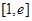 上单调递增
上单调递增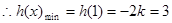 ,解得:
,解得: (不合前提) ---11分
(不合前提) ---11分(Ⅱ)当
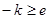 即
即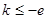 时,
时,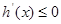 ,此时
,此时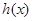 在
在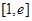 上单调递减
上单调递减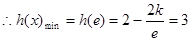 ,解得:
,解得: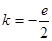 (不合前提)---12分
(不合前提)---12分(Ⅲ)当
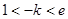 即
即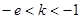 时,
时,当
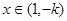 时,
时,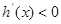 ,
,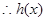 在
在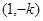 单调递减
单调递减当
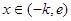 时,
时,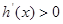 ,
,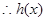 在
在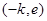 单调递增
单调递增此时
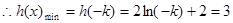 ,解得:
,解得: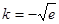 满足前提
满足前提综上可得:
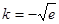

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 为奇函数
为奇函数 的极大值点,
的极大值点, 的解析式;
的解析式; 在曲线
在曲线 上,过点
上,过点 作该曲线的切线,求切线方程.
作该曲线的切线,求切线方程.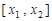
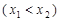 的长度为
的长度为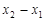 ,已知函数
,已知函数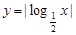 的定义域为
的定义域为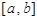 ,值域为
,值域为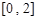 ,则区间
,则区间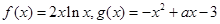 。
。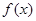 的最小值;
的最小值;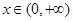 ,使
,使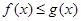 成立,求实数
成立,求实数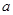 的取值范围。
的取值范围。 ,若f[f(x)]=2,则x的取值范围是( )
,若f[f(x)]=2,则x的取值范围是( )
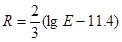 . 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍;
. 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍; 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且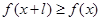 ,则称
,则称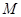 上的
上的 的函数
的函数 时,
时,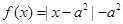 ,且
,且 的取值范围是( )
的取值范围是( )



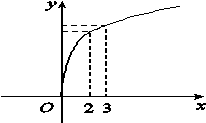




 的导函数是
的导函数是 ,
, ,设
,设 是方程
是方程 的两根,则
的两根,则 的取值范围是 。
的取值范围是 。