题目内容
(本题14分)已知函数, 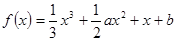
(Ⅰ) 设函数f(x)的图象与x轴交点为A, 曲线y=f(x)在A点处的切线方程是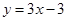 , 求
, 求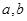 的值;
的值;
(Ⅱ) 若函数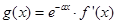 , 求函数
, 求函数 的单调区间.
的单调区间.
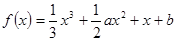
(Ⅰ) 设函数f(x)的图象与x轴交点为A, 曲线y=f(x)在A点处的切线方程是
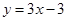 , 求
, 求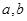 的值;
的值;(Ⅱ) 若函数
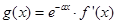 , 求函数
, 求函数 的单调区间.
的单调区间. (Ⅰ)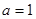 ,
,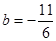 .
.
(Ⅱ)当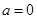 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;
当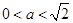 时,
时, 的单调递增区间为
的单调递增区间为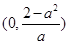 ,单调递减区间为
,单调递减区间为 和
和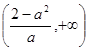 ,
,
当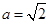 时,
时, 的单调递减区间为
的单调递减区间为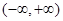 ;
;
当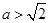 时,
时, 的单调递增区间为
的单调递增区间为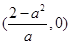 ,单调递减区间为
,单调递减区间为 ,
,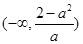 .
.
当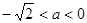 时,
时, 的单调递减区间为
的单调递减区间为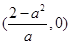 ,单调递增区间为
,单调递增区间为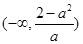 和
和 ,
,
当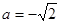 时,
时, 的单调递增区间为
的单调递增区间为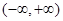 ;
;
当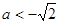 时,
时, 的单调递增区间为
的单调递增区间为 和
和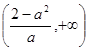 ,单调递减区间为
,单调递减区间为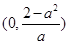 .
.
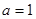 ,
,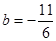 .
.(Ⅱ)当
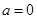 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;当
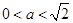 时,
时, 的单调递增区间为
的单调递增区间为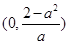 ,单调递减区间为
,单调递减区间为 和
和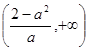 ,
,当
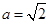 时,
时, 的单调递减区间为
的单调递减区间为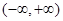 ;
; 当
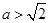 时,
时, 的单调递增区间为
的单调递增区间为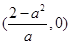 ,单调递减区间为
,单调递减区间为 ,
,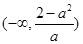 .
. 当
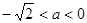 时,
时, 的单调递减区间为
的单调递减区间为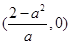 ,单调递增区间为
,单调递增区间为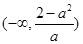 和
和 ,
,当
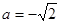 时,
时, 的单调递增区间为
的单调递增区间为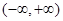 ;
; 当
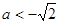 时,
时, 的单调递增区间为
的单调递增区间为 和
和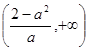 ,单调递减区间为
,单调递减区间为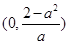 .
. 本试题主要是考查了导数在研究函数中的运用。利用导数的几何意义求解切线方程,利用导数求解函数的单调区间的综合运用。
(1)根据已知条件,可知∵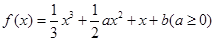 ,∴
,∴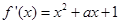
∵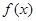 在
在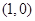 处切线方程为
处切线方程为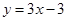 ,
,
∴ ∴
∴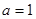 ,
,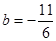 ,求解得到。
,求解得到。
(2)对于参数a分情况讨论。判定导数的符号,确定函数的单调性即可。
解:(Ⅰ)∵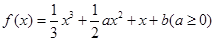 ,
,
∴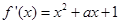 . ……1分
. ……1分
∵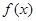 在
在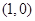 处切线方程为
处切线方程为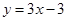 ,
,
∴ , ……3分
, ……3分
∴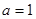 ,
,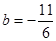 . (各1分) ……5分
. (各1分) ……5分
(Ⅱ)
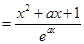
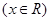 .
.
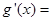
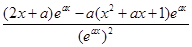
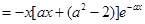 . ……7分
. ……7分
①当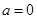 时,
时,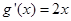 ,
,
 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 . …9分
. …9分
②当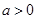 时,令
时,令 ,得
,得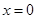 或
或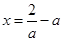 ……10分
……10分
(ⅰ)当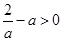 ,即
,即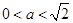 时,
时,
 的单调递增区间为
的单调递增区间为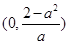 ,单调递减区间为
,单调递减区间为 ,
,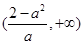 ;---11分
;---11分
(ⅱ)当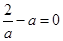 ,即
,即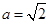 时,
时,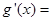
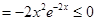 ,
,
故 在
在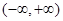 单调递减; ……12分
单调递减; ……12分
(ⅲ)当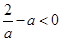 ,即
,即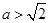 时,
时,
 在
在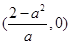 上单调递增,在
上单调递增,在 ,
,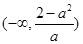 上单调递 …13分
上单调递 …13分
综上所述,当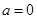 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;
当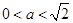 时,
时, 的单调递增区间为
的单调递增区间为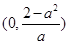 ,单调递减区间为
,单调递减区间为 和
和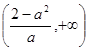 ,
,
当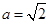 时,
时, 的单调递减区间为
的单调递减区间为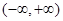 ;
;
当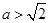 时,
时, 的单调递增区间为
的单调递增区间为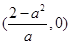 ,单调递减区间为
,单调递减区间为 ,
,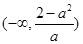 .
.
当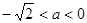 时,
时, 的单调递减区间为
的单调递减区间为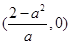 ,单调递增区间为
,单调递增区间为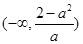 和
和 ,
,
当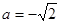 时,
时, 的单调递增区间为
的单调递增区间为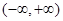 ;
;
当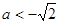 时,
时, 的单调递增区间为
的单调递增区间为 和
和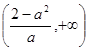 ,单调递减区间为
,单调递减区间为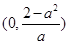
(1)根据已知条件,可知∵
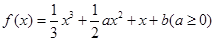 ,∴
,∴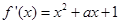
∵
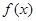 在
在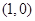 处切线方程为
处切线方程为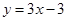 ,
,∴
 ∴
∴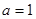 ,
,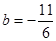 ,求解得到。
,求解得到。(2)对于参数a分情况讨论。判定导数的符号,确定函数的单调性即可。
解:(Ⅰ)∵
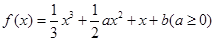 ,
,∴
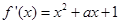 . ……1分
. ……1分∵
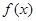 在
在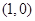 处切线方程为
处切线方程为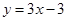 ,
,∴
 , ……3分
, ……3分∴
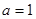 ,
,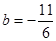 . (各1分) ……5分
. (各1分) ……5分(Ⅱ)

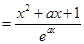
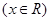 .
.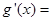
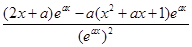
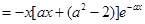 . ……7分
. ……7分①当
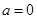 时,
时,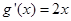 ,
, 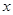 |  | 0 |  |
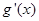 | - | 0 | + |
 |  | 极小值 |  |
 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 . …9分
. …9分②当
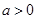 时,令
时,令 ,得
,得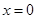 或
或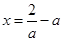 ……10分
……10分(ⅰ)当
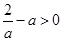 ,即
,即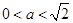 时,
时,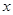 |  | 0 | 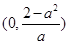 | 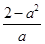 | 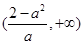 |
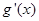 | - | 0 | + | 0 | - |
 |  | 极小值 |  | 极大值 |  |
 的单调递增区间为
的单调递增区间为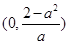 ,单调递减区间为
,单调递减区间为 ,
,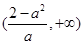 ;---11分
;---11分(ⅱ)当
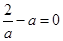 ,即
,即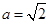 时,
时,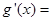
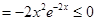 ,
,故
 在
在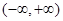 单调递减; ……12分
单调递减; ……12分(ⅲ)当
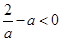 ,即
,即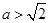 时,
时,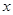 | 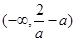 | 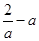 | 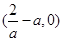 | 0 |  |
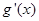 | - | 0 | + | 0 | - |
 |  | 极小值 |  | 极大值 |  |
 在
在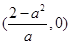 上单调递增,在
上单调递增,在 ,
,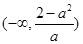 上单调递 …13分
上单调递 …13分综上所述,当
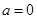 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;当
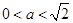 时,
时, 的单调递增区间为
的单调递增区间为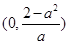 ,单调递减区间为
,单调递减区间为 和
和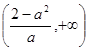 ,
,当
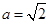 时,
时, 的单调递减区间为
的单调递减区间为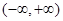 ;
; 当
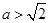 时,
时, 的单调递增区间为
的单调递增区间为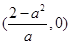 ,单调递减区间为
,单调递减区间为 ,
,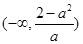 .
. 当
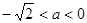 时,
时, 的单调递减区间为
的单调递减区间为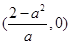 ,单调递增区间为
,单调递增区间为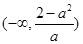 和
和 ,
,当
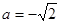 时,
时, 的单调递增区间为
的单调递增区间为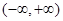 ;
; 当
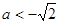 时,
时, 的单调递增区间为
的单调递增区间为 和
和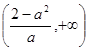 ,单调递减区间为
,单调递减区间为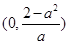

练习册系列答案
相关题目
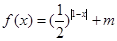 的图象与x轴有公共点,则m的取值范围是 ( )
的图象与x轴有公共点,则m的取值范围是 ( )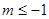
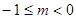

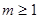
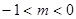
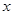 ,
,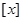 称为取整函数或高斯函数,亦即
称为取整函数或高斯函数,亦即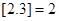 .直角坐标平面内,若
.直角坐标平面内,若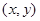 满足
满足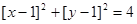 ,则
,则 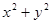 的取值范围是 .
的取值范围是 .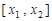
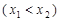 的长度为
的长度为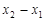 ,已知函数
,已知函数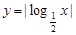 的定义域为
的定义域为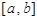 ,值域为
,值域为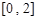 ,则区间
,则区间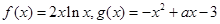 。
。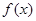 的最小值;
的最小值;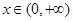 ,使
,使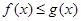 成立,求实数
成立,求实数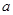 的取值范围。
的取值范围。 与时刻
与时刻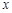 (时) 的关系为
(时) 的关系为 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且 .
. ,
,  ,写出该函数的单调区间,并选择其中一种情形进行证明;
,写出该函数的单调区间,并选择其中一种情形进行证明;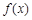 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作 ,求
,求 ,
,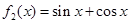 ,
,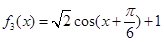 ,
,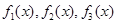 两两为“同形”函数
两两为“同形”函数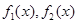 为“同形”函数,且它们与
为“同形”函数,且它们与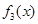 不为“同形”函数
不为“同形”函数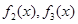 为“同形”函数,且它们与
为“同形”函数,且它们与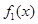 不为“同形”函数
不为“同形”函数 在
在 处取得极值,则
处取得极值,则 的值为()
的值为() 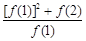 +
+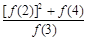 +
+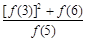 +
+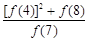 +
+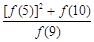 的值为_______________.
的值为_______________.