题目内容
已知双曲线方程 =1(a>b>0),过右焦点F2且倾斜角为60°的线段F2M与y轴交于M,与双曲线交于N,已知
=1(a>b>0),过右焦点F2且倾斜角为60°的线段F2M与y轴交于M,与双曲线交于N,已知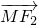 =
= ,则该双曲线的离心率为
,则该双曲线的离心率为
- A.

- B.
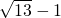
- C.

- D.

C
分析:先求出M的坐标,由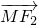 =
= ,求得N的坐标,把N的坐标代入双曲线方程化简求得离心率 e 的大小.
,求得N的坐标,把N的坐标代入双曲线方程化简求得离心率 e 的大小.
解答:线段F2M所在直线的斜率为 tan60°= ,方程为 y-0=
,方程为 y-0= (x-c),
(x-c),
∴M(0,- c). 已知
c). 已知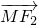 =
= ,设N (m,n ),则 (c,
,设N (m,n ),则 (c, c)=4(c-m,-n),
c)=4(c-m,-n),
∴c=4c-4m, c=-4n,∴m=
c=-4n,∴m= ,n=-
,n=-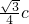 ,∴N(
,∴N( ,-
,-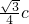 ),
),
把N的坐标代入双曲线方程 =1 得
=1 得  ,
, =1,
=1,
 ,∴9c4-28a2c2+16a4=0,9e4-28e2+16=0,
,∴9c4-28a2c2+16a4=0,9e4-28e2+16=0,
∵e>1,∴e2= =
= ,∴e=
,∴e= ,
,
故选 C.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,求出点N的坐标是解题的关键.
分析:先求出M的坐标,由
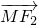 =
= ,求得N的坐标,把N的坐标代入双曲线方程化简求得离心率 e 的大小.
,求得N的坐标,把N的坐标代入双曲线方程化简求得离心率 e 的大小.解答:线段F2M所在直线的斜率为 tan60°=
 ,方程为 y-0=
,方程为 y-0= (x-c),
(x-c),∴M(0,-
 c). 已知
c). 已知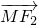 =
= ,设N (m,n ),则 (c,
,设N (m,n ),则 (c, c)=4(c-m,-n),
c)=4(c-m,-n),∴c=4c-4m,
 c=-4n,∴m=
c=-4n,∴m= ,n=-
,n=-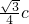 ,∴N(
,∴N( ,-
,-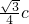 ),
),把N的坐标代入双曲线方程
 =1 得
=1 得  ,
, =1,
=1, ,∴9c4-28a2c2+16a4=0,9e4-28e2+16=0,
,∴9c4-28a2c2+16a4=0,9e4-28e2+16=0,∵e>1,∴e2=
 =
= ,∴e=
,∴e= ,
,故选 C.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,求出点N的坐标是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 =1(a>b>0),过右焦点F2且倾斜角为60°的线段F2M与y轴交于M,与双曲线交于N,已知
=1(a>b>0),过右焦点F2且倾斜角为60°的线段F2M与y轴交于M,与双曲线交于N,已知 =
= ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )


