题目内容
下列函数为偶函数的是
- A.f(x)=|x|+x
- B.
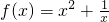
- C.f(x)=x2+x
- D.

D
分析:确定函数的定义域,验证f(-x)与f(x)的关系,即可求得结论.
解答:对于A、函数的定义域为R,f(-x)=|x|-x,∴函数非奇非偶;
对于B、函数的定义域为(-∞,0)∪(0,+∞), ,∴函数非奇非偶;
,∴函数非奇非偶;
对于C、函数的定义域为R,f(-x)=x2-x,∴函数非奇非偶;
对于D、函数的定义域为(-∞,0)∪(0,+∞), ,∴函数为偶函数.
,∴函数为偶函数.
故选D.
点评:本题考查函数的奇偶性,确定函数的定义域,验证f(-x)与f(x)的关系是关键.
分析:确定函数的定义域,验证f(-x)与f(x)的关系,即可求得结论.
解答:对于A、函数的定义域为R,f(-x)=|x|-x,∴函数非奇非偶;
对于B、函数的定义域为(-∞,0)∪(0,+∞),
 ,∴函数非奇非偶;
,∴函数非奇非偶;对于C、函数的定义域为R,f(-x)=x2-x,∴函数非奇非偶;
对于D、函数的定义域为(-∞,0)∪(0,+∞),
 ,∴函数为偶函数.
,∴函数为偶函数.故选D.
点评:本题考查函数的奇偶性,确定函数的定义域,验证f(-x)与f(x)的关系是关键.

练习册系列答案
相关题目
下列函数为偶函数的是( )
A、f(x)=
| ||
B、f(x)=ln
| ||
C、f(x)=
| ||
| D、f(x)=|x| |