题目内容
已知函数 ,
,
(1)
(2)是否存在实数 ,使
,使 在
在 上的最小值为
上的最小值为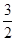 ,若存在,求出
,若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
 ,
, (1)

(2)是否存在实数
 ,使
,使 在
在 上的最小值为
上的最小值为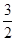 ,若存在,求出
,若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。(1)-1
(2) 存在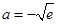 ,使
,使 在
在 上的最小值为
上的最小值为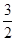
(2) 存在
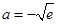 ,使
,使 在
在 上的最小值为
上的最小值为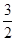
试题分析:解:(1)
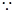
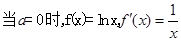 . 1分
. 1分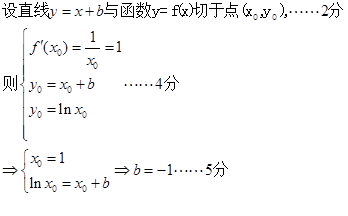
(2)假设存在实数
 ,使
,使 在
在 上的最小值为
上的最小值为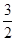 ,
,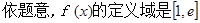 .
.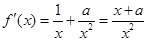 ………6分
………6分令
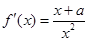 =0,得
=0,得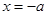 ………7分
………7分下面就
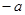 与区间
与区间 的相对位置讨论,
的相对位置讨论,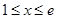
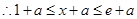
① 若
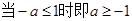 ,则
,则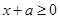 ,
,即
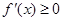 在
在 上恒成立,此时
上恒成立,此时 在
在 上为增函数, 8分
上为增函数, 8分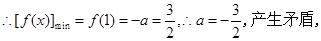 (舍去). 9分
(舍去). 9分② 若
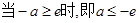 ,则
,则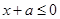 ,即
,即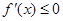 在
在 上恒成立,
上恒成立,此时
 在
在 上为减函数, 10分
上为减函数, 10分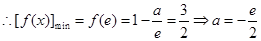 (舍去).………11分
(舍去).………11分③ 若
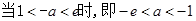 , (方法1):列表如下
, (方法1):列表如下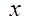 | 1 | 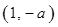 | 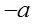 | 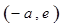 | 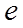 |
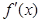 | | 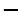 | 0 | 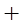 | |
 | 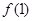 | ↙ | 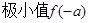 | ↗ | 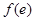 |
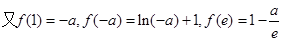 ………12分
………12分
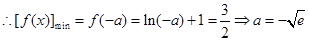 ………13分
………13分综上可知:存在
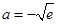 ,使
,使 在
在 上的最小值为
上的最小值为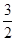 ………14分
………14分(方法2):当
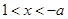 时,
时,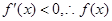 在
在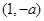 上为减函数,
上为减函数,当
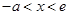 时,
时,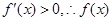 在
在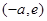 上为增函数,………12分
上为增函数,………12分
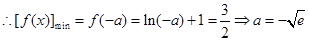 , ………13分
, ………13分综上可知:存在
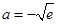 ,使
,使 在
在 上的最小值为
上的最小值为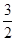 ………14分
………14分点评:考查了导数的几何意义,以及运用导数的知识求解函数的最值问题,属于基础题。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
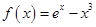 ,
,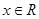 ,则函数的极值点的个数是( )
,则函数的极值点的个数是( )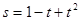 其中
其中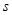 的单位是米,
的单位是米,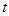 的单位是秒,那么物体在
的单位是秒,那么物体在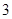 秒末的瞬时速度是( )
秒末的瞬时速度是( ) 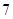 米/秒
米/秒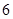 米/秒
米/秒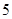 米/秒
米/秒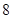 米/秒
米/秒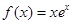 .
.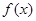 的单调区间与极值;
的单调区间与极值;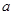 ,使得对任意的
,使得对任意的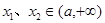 ,当
,当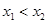 时恒有
时恒有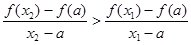 成立.若存在,求
成立.若存在,求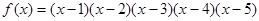 则
则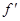
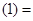
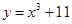 在点P(1,12)处的切线与两坐标轴围成三角形的面积是
在点P(1,12)处的切线与两坐标轴围成三角形的面积是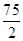
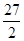
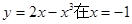 处的切线方程为( )
处的切线方程为( )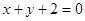
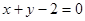
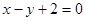
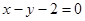
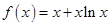 .
.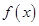 的图像在点
的图像在点 处的切线方程;
处的切线方程;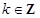 ,且
,且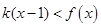 对任意
对任意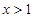 恒成立,求
恒成立,求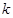 的最大值;
的最大值;