题目内容
设直线l的方程为:x+ysinθ-2013=0(θ∈R),则直线l的倾斜角α的范围是( )
分析:当sinθ=0时,直线l的斜率不存在,倾斜角α=
,当sinθ≠0时,直线l的斜率k=-
结合正弦函数的值域及反比例函数的性质,可以分析出直线l的斜率k的取值范围,进而得到倾斜角的范围,综合讨论结果,可得答案.
| π |
| 2 |
| 1 |
| sinθ |
解答:解:当sinθ=0时,直线l的方程为:x-2013=0
此时倾斜角α=
当sinθ≠0时,直线l的方程为:y=-
x+2013
直线l的斜率k=-
∈(-∞,-1]∪[1,+∞)
直线l的倾斜角α∈[
,
)∪(
,
]
综上所述:直线l的倾斜角α∈[
,
]
故选C
此时倾斜角α=
| π |
| 2 |
当sinθ≠0时,直线l的方程为:y=-
| 1 |
| sinθ |
直线l的斜率k=-
| 1 |
| sinθ |
直线l的倾斜角α∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
综上所述:直线l的倾斜角α∈[
| π |
| 4 |
| 3π |
| 4 |
故选C
点评:本题考查的知识点是直线的方程,直线斜率与倾斜角的关系,解答时易忽略直线l的斜率不存在,倾斜角α=
,而错选D.
| π |
| 2 |

练习册系列答案
相关题目
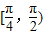
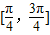
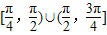
 的焦点为F1.
的焦点为F1. ,又因为
,又因为 ,这样可知得到
,这样可知得到 。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到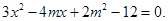 ,再利用
,再利用 可以结合韦达定理求解得到m的值和圆p的方程。
可以结合韦达定理求解得到m的值和圆p的方程。
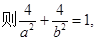 ①………………………………1分
①………………………………1分
 ………………………7分
………………………7分 、
、 ………………8分
………………8分
 ………………………9分
………………………9分 ……………………………10分
……………………………10分