题目内容
(2012•浦东新区三模)已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是y=±
x,双曲线过点P(6,6).
(1)求双曲线方程
(2)动直线l经过△A1PA2的重心G,与双曲线交于不同的两点M、N,问是否存在直线l,使G平分线段MN,证明你的结论.
2
| ||
| 3 |
(1)求双曲线方程
(2)动直线l经过△A1PA2的重心G,与双曲线交于不同的两点M、N,问是否存在直线l,使G平分线段MN,证明你的结论.
分析:(1)设出双曲线方程,利用渐近线方程是y=±
x,双曲线过点P(6,6),建立方程组,求出几何量,即可得到双曲线的方程;
(2)利用点差法,结合韦达定理求出直线方程,利用判别式进行验证,即可得到结论.
2
| ||
| 3 |
(2)利用点差法,结合韦达定理求出直线方程,利用判别式进行验证,即可得到结论.
解答: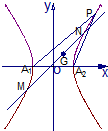 解:(1)如图,设双曲线方程为
解:(1)如图,设双曲线方程为
-
=1…(1分)
由已知渐近线方程是y=±
x,双曲线过点P(6,6),得
…(3分)
解得
…(5分)
所以所求双曲线方程为
-
=1 …(6分)
(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)…(8分)
假设存在直线l,使G(2,2)平分线段MN,
设M(x1,y1),N(x2,y2) 则有x1+x2=4,y1+y2=4
∵
-
=1,
-
=1
∴两式相减可得
=
,∴kl=
…(10分)
∴l的方程为y=
(x-2)+2(12分)
代入椭圆方程,消去y,整理得x2-4x+28=0
∵△=16-4×28<0,∴所求直线l不存在 …(14分)
 解:(1)如图,设双曲线方程为
解:(1)如图,设双曲线方程为| x2 |
| a2 |
| y2 |
| b2 |
由已知渐近线方程是y=±
2
| ||
| 3 |
|
解得
|
所以所求双曲线方程为
| x2 |
| 9 |
| y2 |
| 12 |
(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)…(8分)
假设存在直线l,使G(2,2)平分线段MN,
设M(x1,y1),N(x2,y2) 则有x1+x2=4,y1+y2=4
∵
| x12 |
| 9 |
| y12 |
| 12 |
| x22 |
| 9 |
| y22 |
| 12 |
∴两式相减可得
| y1-y2 |
| x1-x2 |
| 4 |
| 3 |
| 4 |
| 3 |
∴l的方程为y=
| 4 |
| 3 |
代入椭圆方程,消去y,整理得x2-4x+28=0
∵△=16-4×28<0,∴所求直线l不存在 …(14分)
点评:本题考查双曲线的标准方程,考查点差法的运用,考查学生方程解决问题的能力,正确运用点差法是关键.

练习册系列答案
相关题目
 (2012•浦东新区二模)手机产业的发展催生了网络新字“孖”.某学生准备在计算机上作出其对应的图象,其中A(2,2),如图所示.在作曲线段AB时,该学生想把函数
(2012•浦东新区二模)手机产业的发展催生了网络新字“孖”.某学生准备在计算机上作出其对应的图象,其中A(2,2),如图所示.在作曲线段AB时,该学生想把函数