题目内容
14.已知数列{an}是各项均为正数的等差数列,且lga1,lga2,lga4成等差数列,若bn=$\frac{1}{{a}_{{2}^{n}}}$(n=1,2,3,…),求证:数列{bn}为等比数列.分析 根据等差数列的定义和性质,建立方程关系,利用等比数列的定义进行证明即可.
解答 证明:∵数列{an}是各项均为正数的等差数列,且lga1,lga2,lga4成等差数列,
若公差d≠0时,lga1+lga4=2lga2,
即lga1a4=lga22,
即a1a4=a22,
则a1(a1+3d)=(a1+d)2,
解得a1=d,则an=a1+(n-1)d=na1,(a1>0),
则当n≥2时,$\frac{{b}_{n}}{{b}_{n-1}}$=$\frac{{a}_{{2}^{n-1}}}{{a}_{{2}^{n}}}$=$\frac{{2}^{n-1}{a}_{1}}{{2}^{n}{a}_{1}}$=$\frac{1}{2}$为常数,
故数列{bn}为等比数列.
当公差d=0时,也满足条件.
点评 本题主要考查等比数列的证明以及等差数列的应用,利用定义法是解决本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2.下列结论正确的是( )
| A. | 若直线l∥平面α,直线l∥平面β,则α∥β. | |
| B. | 若直线l⊥平面α,直线l⊥平面β,则α∥β. | |
| C. | 若直线l1,l2与平面α所成的角相等,则l1∥l2 | |
| D. | 若直线l上两个不同的点A,B到平面α的距离相等,则l∥α |
9.定积分${∫}_{0}^{1}$(3$\sqrt{x}$-$\sqrt{1-{x}^{2}}$)dx等于( )
| A. | $\frac{8-π}{4}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{2-π}{2}$ | D. | $\frac{4-π}{8}$ |
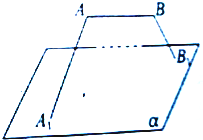 线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.
线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.